Problemas de interpolación
1
Nivel
Primer ciclo
Dificultad
5
Dado que 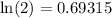 ,
, 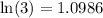 y
y 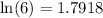 , interpole con un polinomio de Lagrange el logaritmo natural de cada entero desde 1 hasta 10. Tabule lo anterior junto con el error en cada punto.
, interpole con un polinomio de Lagrange el logaritmo natural de cada entero desde 1 hasta 10. Tabule lo anterior junto con el error en cada punto.
Solución disponible
nicco
Los polinomios de interpolación de Lagrange se calculan a partir de la siguiente fórmula:
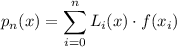
(1)
donde 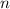 es el grado del polinomio y
es el grado del polinomio y
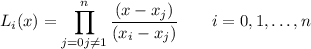
(2)
Disponemos del siguiente conjunto de datos:
| i | 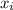 |
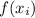 |
|---|---|---|
| 0 | 2 | 0.69315 |
| 1 | 3 | 1.09860 |
| 2 | 6 | 1.79180 |
Por tanto, aplicando las fórmulas (1) y (2) interpolaremos con un polinomio de Lagrange el logaritmo natural de cada entero desde 1 hasta 10. Los valores obtenidos se detallan en la siguiente tabla junto con el error en cada punto, que viene dado por 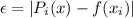 :
:
| i | 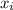 |
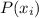 |
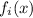 |
 |
|---|---|---|---|---|
| 0 | 2 | 0.693150 | 0.693150 | 0.000000 |
| 1 | 3 | 1.098600 | 1.098600 | 0.000000 |
| 2 | 6 | 1.791800 | 1.791800 | 0.000000 |
| 3 | 1 | 0.200531 | 0.000000 | 0.200531 |
| 4 | 4 | 1.416886 | 1.386294 | 0.030592 |
| 5 | 5 | 1.647930 | 1.609438 | 0.038492 |
| 6 | 7 | 1.848506 | 1.945910 | 0.097404 |
| 7 | 8 | 1.772935 | 2.079441 | 0.306506 |
| 8 | 9 | 1.700275 | 2.197224 | 0.496949 |
| 9 | 10 | 1.495406 | 2.302585 | 0.807179 |
Como podemos comprobar observando los valores tabulados, el error es mayor para puntos fuera del intervalo 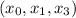 a los que se extrapola el polinomio.
a los que se extrapola el polinomio.


