Problemas de integración por residuos
1
Integración por residuos
Nivel
Primer ciclo
Dificultad
5
Solución disponible
Tupaka
Teniendo en cuenta que el integrando es una función par, y que el coseno es la parte real de una exponencial compleja, podemos reescribir la integral de la forma
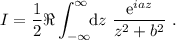
(1)
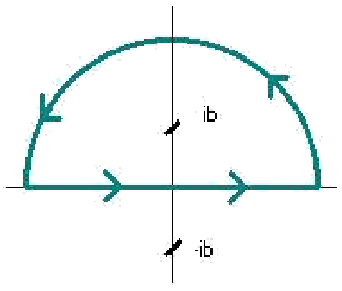
En el límite 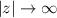 , el integrando tiende a cero. Por lo tanto, podemos substituir el circuito de integración por el mostrado en la siguiente imagen:
, el integrando tiende a cero. Por lo tanto, podemos substituir el circuito de integración por el mostrado en la siguiente imagen:
La función tiene residuos en 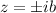 . El único que nos influye es el situado en el semiplano superior, por lo que podemos escribir
. El único que nos influye es el situado en el semiplano superior, por lo que podemos escribir
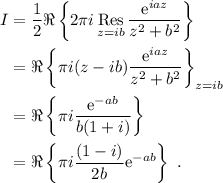
(2)
Por lo tanto,
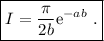
(3)

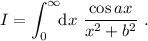

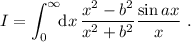
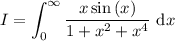
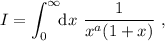
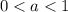 .
.