Problemas de integración
Nivel: Primer ciclo
Sean las integrales
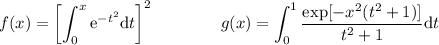
1.Demostrad que 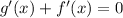 y que
y que 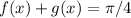
2.A continuación,teniendo en cuenta que 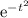 es una función con simetría par,utilizad este resultado para mostrar que
es una función con simetría par,utilizad este resultado para mostrar que
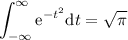
Tenemos que demostrar que
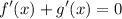
Para ello, vamos a derivar ambas funciones por separado:
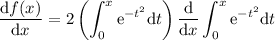
Por el primer teorema fundamental del cálculo sabemos que 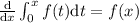 , con lo cual
, con lo cual
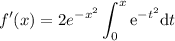
Y, ahora, derivamos 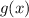 :
:
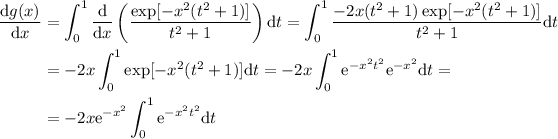
Podemos hacer el siguiente cambio de variable: 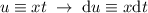 , con el cual, los límites de integración quedan
, con el cual, los límites de integración quedan 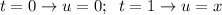 . Es decir, que
. Es decir, que
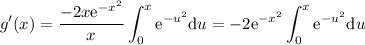
Ahora, si sumamos f'(x) y g'(x), teniendo en cuenta que u y t son variables mudas (podemos designar a ambas con la letra v), nos queda
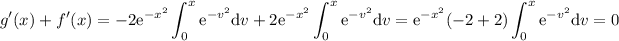
como queríamos demostrar.
Ahora bien, si 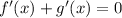 , integrando, vemos que
, integrando, vemos que
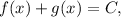
para obtener el valor de la constante, hacemos 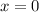 y tenemos que
y tenemos que
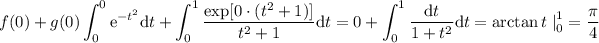
es decir, que
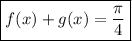
Con lo que hemos obtenido en el apartado anterior, podemos calcular cuánto vale 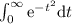 , luego, como
, luego, como 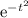 es una función par, bastará con multiplicar el resultado obtenido por 2 para saber cuánto vale
es una función par, bastará con multiplicar el resultado obtenido por 2 para saber cuánto vale 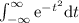 .
.
Sabemos que
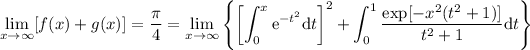
Con lo cual
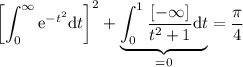
y por lo tanto
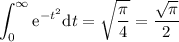
Debido a la propiedad simétrica de la función que teníamos como dato:
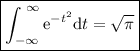
Sea la función 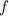 definida mediante
definida mediante
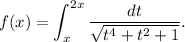
Estudiar las asíntotas y la monotonía de 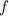 . Dibujar aproximadamente la gráfica de
. Dibujar aproximadamente la gráfica de 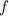 .
.

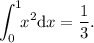

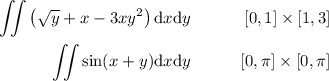
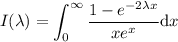
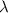 (siendo
(siendo 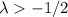 )
)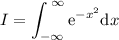
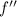 es continua y que
es continua y que 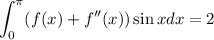 . Sabiendo que
. Sabiendo que 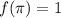 , calcule
, calcule 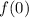 .
.