Problemas de inducción matemática
Utiliza el principio de inducción para demostrar que la suma de los primeros N números enteros es 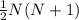 . Es decir,
. Es decir,
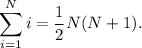
Paso 1. Demostramos que la desigualdad es cierta para n=1,
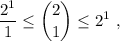
realizando las operaciones indicadas, vemos que todos los miembros dan como resultado 2. Por lo tanto, la inecuación para n=1 es cierta.
Paso 2. Suponemos que, por hipótesis, la inecuación se cumple para n arbitrario,
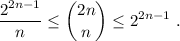
Paso 3. Utilizando la ecuación (2), debemos demostrar que la inecuación se cumple para n+1,
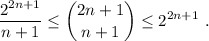
Debemos manipular (3) para que se parezca lo más posible a (2). Podemos aplicar las siguientes propiedades,
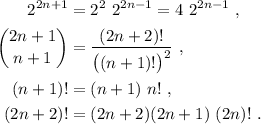
Substituyendo en (3),
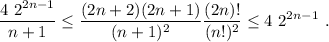
Para que el primer miembro se parezca lo más posible al de (2), podemos multiplicar y dividir por n. En el segundo miembro, podemos reconocer directamente la definición de 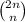 . Por lo tanto, tenemos
. Por lo tanto, tenemos
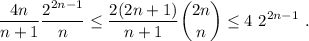
Para continuar, debemos utilizar el siguiente hecho: dados dos cantidades tales que 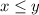 , entonces la relación
, entonces la relación
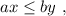
es cierta si 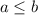 . Demostrar este hecho es sencillo. Si
. Demostrar este hecho es sencillo. Si 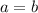 , entonces ambos factores cancelan y recuperamos la desigualdad inicial. Si
, entonces ambos factores cancelan y recuperamos la desigualdad inicial. Si 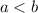 , entonces
, entonces 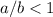 y (7) se puede reescribir
y (7) se puede reescribir
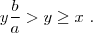
Armados con este hecho, podemos ver que la primera desigualdad de (6) es cierta si
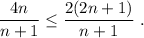
Simplificando los denominadores, esta condición se reduce a 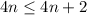 , lo cual es obviamente cierto.
, lo cual es obviamente cierto.
Por otra parte, la segunda desigualdad en (6) se cumplirá si
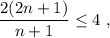
que se reduce a 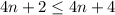 , que de nuevo es cierto para todo n.
, que de nuevo es cierto para todo n.

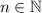 , se cumple
, se cumple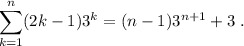

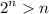 .
.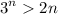 .
.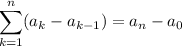 .
.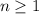
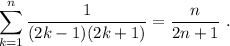
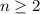 , se cumple
, se cumple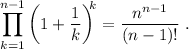
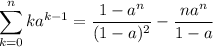
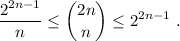
 , terminan en seis.
, terminan en seis.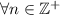 se cumple:
se cumple: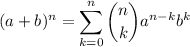
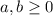 demostrar que para todo
demostrar que para todo 
