Problemas de hamilton-jacobi
Utiliza la ecuación de Hamilton-Jacobi para resolver el movimiento de un oscilador armónico de masa 
y frecuencia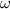 
, en una dimensión.
El hamiltoniano del oscilador armónico es
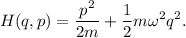
La ecuación de Hamilton-Jacobi se escribe de la forma
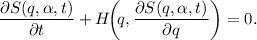
En este caso concreto, la ecuación de Hamilton-Jacobi toma la forma,
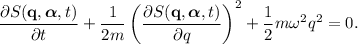
Dado que el oscilador armónico es conservativo, podemos ensayar la siguiente solución
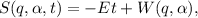
donde la energía, E, juega el papel de la constante del movimiento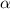 
. En estas condiciones la ecuación (3) se escribe de la forma
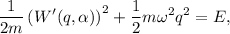
donde la prima representa derivación respecto de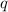 
. A partir de la ecuación (5) podemos aislar la derivada de la función característica en función de las constantes del movimiento y de ,
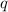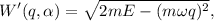
de donde obtenemos
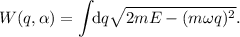
La integral anterior se puede resolver fácilmente, aunque por ahora no lo necesitamos.
Las ecuaciones del movimiento se encuentran mediante las relaciones
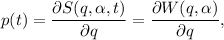
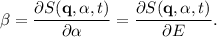
De la ecuación (8) tenemos
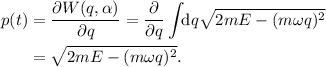
De la ecuación (9) obtenemos
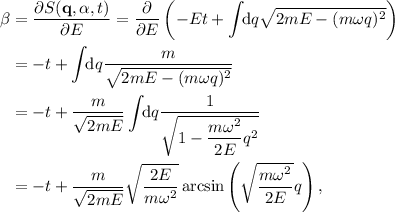
de donde podemos aislar la coordenada en función del tiempo
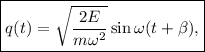
de donde vemos que un oscilador armónico realiza oscilaciones senosoidales con pulsación 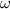y una amplitud proporcional a la raíz cuadrada de la energía total, y con una fase inicial dada por 
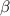. Por último, utilizando la ecuación (10), podemos encontrar el momento conjugado en función del tiempo,
