Problemas de geometría diferencial
Considerad la superficie de un toro de radios  y
y  coordenado con los ángulos
coordenado con los ángulos 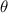 i
i 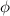 .
.
1.El vector 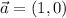 en el punto
en el punto 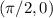 se transporta paralelamente a lo largo de la curva
se transporta paralelamente a lo largo de la curva 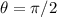 . ¿Cuáles son las componentes del vector transportado al punto
. ¿Cuáles son las componentes del vector transportado al punto 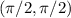 ?
?
2.Repetid el cálculo con el vector 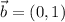 cuando se transporta paralelamente de
cuando se transporta paralelamente de 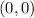 a
a 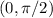 a lo largo de la curva
a lo largo de la curva 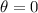 .
.
Antes de empezar a calcular símbolos de Christoffel como condenados vamos a establecer la estrategia a seguir para resolver el problema. Nos piden que transportemos paralelamente un vector a lo largo de una curva determinada, que es equivalente a imponer que su derivada covariante a lo largo de dicha curva se anule. Es decir, si nuestro vector es 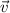 y el vector tangente a la curva en cuestión es
y el vector tangente a la curva en cuestión es 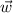 , entonces debemos imponer:
, entonces debemos imponer:
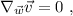
que en componentes se escribe:
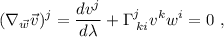
donde 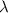 es el parámetro de la curva definida por
es el parámetro de la curva definida por 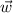 .
.
Esto nos da una ecuación diferencial para cada una de las componentes del vector 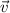 (una para cada valor del índice
(una para cada valor del índice 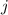 ). Si las integramos obtendremos para cada componente una solución del tipo
). Si las integramos obtendremos para cada componente una solución del tipo 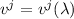 . Estas soluciones nos dan, para cada punto de la curva, cuáles tienen que ser las componentes de
. Estas soluciones nos dan, para cada punto de la curva, cuáles tienen que ser las componentes de 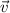 para que éste sea transportado paralelamente hasta ese punto. Por lo tanto, dando valores a
para que éste sea transportado paralelamente hasta ese punto. Por lo tanto, dando valores a 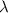 obtendremos las componentes del tranporte paralelo de
obtendremos las componentes del tranporte paralelo de 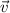 en ese punto de la curva, que es lo que nos piden que calculemos.
en ese punto de la curva, que es lo que nos piden que calculemos.
Y ahora vayamos a por los cálculos explícitos. Los más avispados ya habrán reparado en la necesidad de conocer los símbolos de Christoffel, 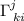 , para poder resolver las ecuaciones (2). Lo más común es calcularlos a partir de la métrica de nuestra variedad mediante la conocida fórmula:
, para poder resolver las ecuaciones (2). Lo más común es calcularlos a partir de la métrica de nuestra variedad mediante la conocida fórmula:
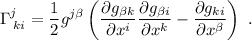
donde las 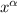 se refieren a las coordenadas que estemos utilizando (en nuestro caso será
se refieren a las coordenadas que estemos utilizando (en nuestro caso será 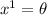 y
y 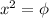 ). Daros buena cuenta de que hay una suma en el índice
). Daros buena cuenta de que hay una suma en el índice 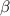 !
!
Por lo tanto vamos a calcular en primer lugar el tensor métrico 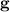 a partir de las ecuaciones que definen nuestra variedad (ver figura 1):
a partir de las ecuaciones que definen nuestra variedad (ver figura 1):
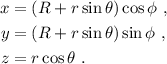
Los vectores base en las coordenadas 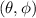 son:
son:
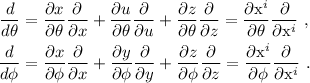
Calculamos las componentes de la métrica a partir de la definición:
En este desarrollo hemos utilizado la multilinealidad del tensor métrico y el hecho conocido de que en la base cartesiana tenemos 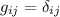 , como se indica en los corchetes horizontales inferiores.
, como se indica en los corchetes horizontales inferiores.
Procediendo igual que en el caso anterior obtenemos:
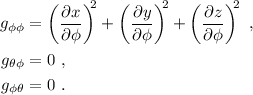
Finalmente, encontramos explícitamente 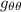 y
y 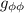 calculando las parciales
calculando las parciales 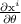 y
y 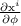 (recordemos que
(recordemos que 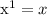 ,
, 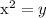 ,
, 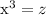 ):
):
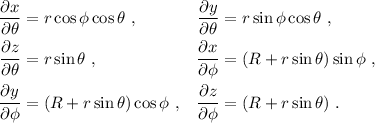
Introduciendo estos resultados en la expresión para 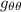 i
i 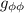 nos queda:
nos queda:
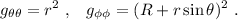
Con lo cual:
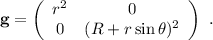
Ahora ya podemos calcular los símbolos de Christoffel mediante la ecuación (3), teniendo en cuenta que 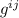 es la componente
es la componente 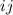 de la inversa de
de la inversa de 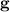 . En nuestro caso, como
. En nuestro caso, como 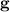 es diagonal tenemos:
es diagonal tenemos:
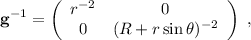
y por lo tanto
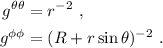
Vamos pues a por los símbolos de Christoffel. Lo primero que debemos ver para ahorrarnos algunos cálculos es que en la suma sobre el índice 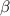 en la ecuación (3), solamente sobrevivirá el sumando correspondiente a
en la ecuación (3), solamente sobrevivirá el sumando correspondiente a 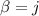 porque
porque 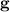 es diagonal y por lo tanto
es diagonal y por lo tanto 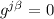 para
para 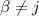 . Además, si examinamos la ecuación (3) podemos ver que, si
. Además, si examinamos la ecuación (3) podemos ver que, si 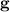 es simétrica (y en nuestro caso lo es), los símbolos de Christoffel también serán simétricos respecto a los dos subíndices
es simétrica (y en nuestro caso lo es), los símbolos de Christoffel también serán simétricos respecto a los dos subíndices 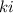 , pues nos damos cuenta de que al hacer la permutación
, pues nos damos cuenta de que al hacer la permutación 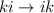 intercambiamos el orden de los dos primeros sumandos de (3), lo cual no afecta al resultado, a la vez que pasamos de
intercambiamos el orden de los dos primeros sumandos de (3), lo cual no afecta al resultado, a la vez que pasamos de 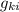 a
a 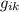 en el tercero, que tampoco nos afecta por ser
en el tercero, que tampoco nos afecta por ser 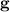 simétrica. Por lo tanto:
simétrica. Por lo tanto:
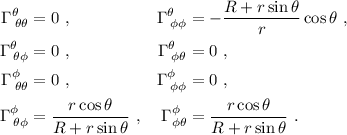
Y con todo esto por fin podemos calcular las ecuaciones (2).
Para el primer caso tenemos:
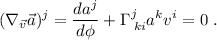
Esto nos da las siguientes dos ecuaciones (una para cada valor del índice 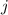 ), en las que hemos desarrollado la suma en
), en las que hemos desarrollado la suma en 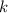 e
e  :
:
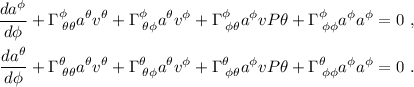
En cada una de las ecuaciones podemos eliminar términos si consideramos que algunas de las 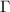 son nulas, según hemos calculado más arriba, y si nos damos cuenta de que
son nulas, según hemos calculado más arriba, y si nos damos cuenta de que 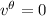 y
y 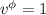 , pues
, pues 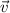 es el vector tangente a la curva. Por lo tanto las dos ecuaciones anteriores quedan reducidas a:
es el vector tangente a la curva. Por lo tanto las dos ecuaciones anteriores quedan reducidas a:
pero como estamos en una curva en la que constantemente 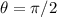 :
:
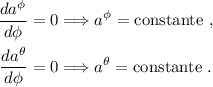
por lo tanto las componentes de 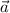 no cambian al transportarlo paralelamente a lo largo de la curva indicada en el primer apartado.
no cambian al transportarlo paralelamente a lo largo de la curva indicada en el primer apartado.
En el segundo apartado debemos proceder exactamente igual. El vector tangente a la curva es el mismo de antes, pero en este caso tenemos que 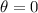 . Las ecuaciones quedan:
. Las ecuaciones quedan:
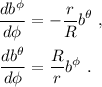
Para resolver este sistema hay que desacoplarlo. En este caso es sencillo. En primer lugar derivamos las ecuaciones (18) para obtener:
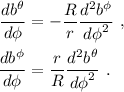
Ahora introducimos el resultado de (19) en (18) para obtener las ecuaciones del oscilador armónico simple:
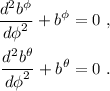
Las soluciones son archiconocidas:
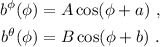
Para determinar las constantes 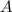 ,
,  ,
, 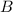 y
y 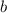 necesitamos conocer las funciones y sus derivadas en algún punto (por ejemplo en
necesitamos conocer las funciones y sus derivadas en algún punto (por ejemplo en 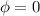 ). Del enunciado tenemos que
). Del enunciado tenemos que 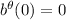 y
y 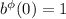 . Y de las ecuaciones (1.3) y (1.4) encontramos que:
. Y de las ecuaciones (1.3) y (1.4) encontramos que:
Con todo esto encontramos que 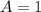 ,
, 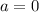 ,
, 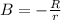 y
y 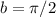 (no creo necesario explicitar el cálculo realizado para llegar a estos resultados). Por lo tanto:
(no creo necesario explicitar el cálculo realizado para llegar a estos resultados). Por lo tanto:
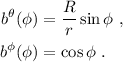
Para 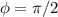 vemos que:
vemos que:
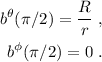
Y este resultado completa nuestro problema.



