Problemas de física de fluidos
Dos vasos comunicantes contienen un líquido de densidad conocida. Las áreas de las secciones rectas de las vasijas son A y 3A. Determinar el cambio de altura del nivel del líquido si un objeto de masa m y una densidad de 0.8 veces la del líquido se introduce en una de las vasijas.
La clepsidra es un recipiente con simetría de revolución en la cual se coloca agua y posee un agujero pequeño en la parte inferior. Al ir vaciándose el agua la altura de esta indica el tiempo que transcurre. ¿Cuál debe de ser la forma de la curva generatriz para que la altura del agua sea lineal con el tiempo?
Un contenedor semiesférico de radio 
se llena con agua. La parte superior está abierta a la presión atmosférica. En la parte inferior existe un tapón abierto de radio mucho menor que . Halle el tiempo total necesario para vaciar el contenedor. Supóngase que el flujo es ideal.
Suponiendo que el líquido ya ha empezado a descender, y llamando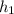 
a la distancia entre el fondo y la altura máxima que alcanza el fluido en el contenedor (por tanto asignando al tapón altura nula), se tiene que la ecuación de Bernoulli toma el siguiente aspecto
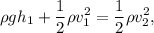
donde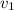 
es la velocidad con la que cambia la altura del fluido en el contenedor y 
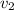es la velocidad con la que sale el fluido por el tapón. Admitiendo a continuación la hipótesis de régimen cuasiestacionario, podemos realizar la aproximación 
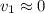, es decir, la altura varía muy lentamente con respecto al tiempo, se tiene que
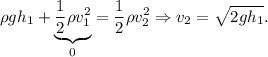
Por otra parte, la ecuación de continuidad aplicada a los puntos de altura 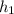y al tapón nos dice que
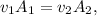
donde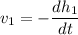 
(el signo negativo se debe a que la altura disminuye con el tiempo), 
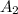es el área del tapón, 
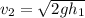como ya hemos obtenido antes, y 
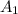es el área que cubre el fluido a altura 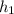. Como sabemos que el fluido está contenido en un contenedor semiesférico, el área 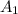será una función del tipo 
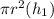, donde se puede comprobar que 
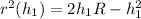. Luego 
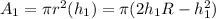y obtenemos la siguiente ecuación diferencial
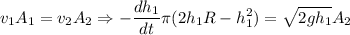
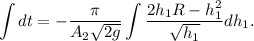
En el instante inicial, la altura era el radio de la semiesfera, y en el instante de vaciado total, la altura es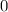 
, por tanto
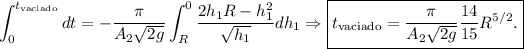
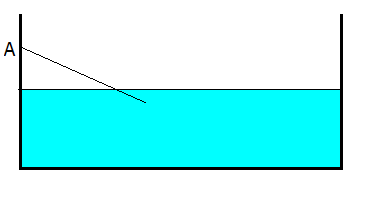
Una barra delgada y homogénea, de longitud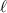 
y de densidad volumétrica de masa 
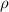, se encuentra sujeta por un extremo de un punto A, mientras que el otro extremo está sumergido en un líquido de densidad 
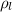. La barra puede moverse libremente alrededor de un eje perpendicular al plano de la figura y que pasa por A. ¿Qué porcentaje de longitud de la barra se halla sumergida, en la posición de equilibrio estable?
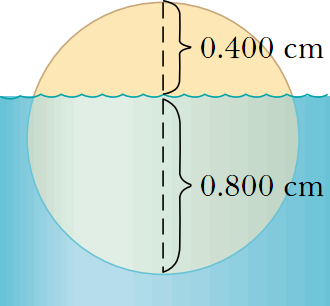
Una bola sólida y homogénea de diámetro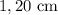 
está sumergida parcialmente en agua tal y como se muestra en la figura, y está en equilibrio. Determine su densidad.
Una bomba hidráulica de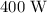 
de potencia útil es capaz de extraer el líquido contenido en un depósito con forma semiesférica en 
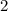minutos. Determinar la densidad del líquido sabiendo que el radio de la semiesfera es de 
.
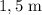Problema propuesto en examen de oposiciones a profesor de secundaria, especialidad Física y Química. Castilla-La Mancha, 2002.
