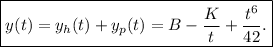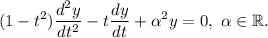Problemas de ecuaciones diferenciales ordinarias
Encontrar la solución general de las siguientes ecuaciones diferenciales.
1.
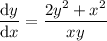
2.
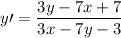
3.
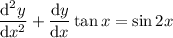
4.
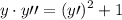
Para resolver la ecuación diferencial
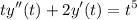
1.Obtenga la solución general de la ecuación diferencial homogénea asociada.
2.Demuestre la identidad
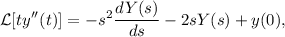
donde 
representa la transformada de Laplace.
3.Aplique transformadas de Laplace a la ecuación diferencial original y obtenga, de este modo, una solución particular.
4.Finalice mostrando la solución general obtenida.
La ecuación diferencial homogénea asociada es
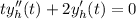
Si definimos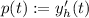 
obtenemos que
Recordando que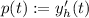
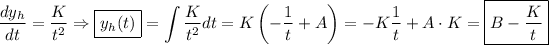
donde 
.
Recordando que
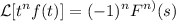
donde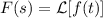 
, tenemos como caso particular que
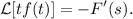
De esta manera,
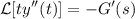
donde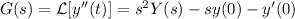 
. Derivamos y cambiamos de signo:
que es lo que queríamos demostrar.
Sustituyendo el resultado obtenido en el apartado anterior, y recordando que
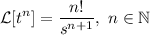
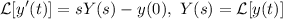
tenemos que
Integrando
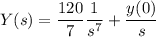
donde no se ha tenido en cuenta la constante de integración porque sólo nos interesa una de las primitivas de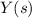 
. Invirtiendo la transformada obtenemos la solución particular pedida
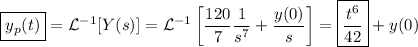
Sólo hemos tomado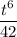 
como solución particular ya que la solución particular es única salvo soluciones particulares de la homogénea asociada, y la constante 
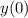es solución de la homogénea asociada.
La teoría de ecuaciones diferenciales ordinarias lineales nos dice que la solución general de una EDO lineal no homogénea posee estructura de subespacio afín, es decir, la solución general es suma de una solución particular de la ecuación completa más la general de la homogénea asociada. Hemos determinado esta última en el primer apartado, y la particular en el tercer apartado, por lo que podemos concluir que
