Problemas de dinámica de la rotación
Nivel: Secundaria
Dada una fuerza de módulo 3N, aplicada en el punto (1,3,1) y tal que forma ángulos de 30º y 60º con los ejes X e Y, respectivamente. Halla su momento con respecto al punto (5,2,1).
Un cuerpo de 500g gira sobre una superficie horizontal sin rozamiento, atado por una cuerda de 80cm de longitud a una punta. Calcula la fuerza que soporta la cuerda cuando el cuerpo gira a 60rpm.
Un carro de 1T avanza horizontalmente y sin rozamiento sobre un carril con una velocidad inicial de 10m/s en el punto A, según expresa la figura. A continuación entra en un lazo vertical de 4m de radio.
Calcular:
1.La fuerza que ejerce el carril sobre el carro al pasar por el punto B (a media altura).
2.Velocidad mínima necesaria en A para que el carro alcance el punto C (cima del lazo) sin despegarse del carril.
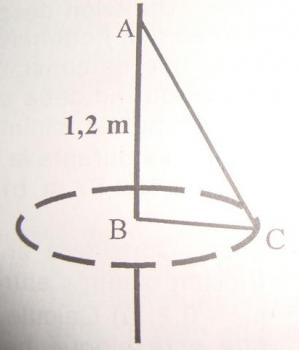
Un cuerpo de 50g colgado de un hilo de 1,2m de longitud describe una circunferencia de 0,5m de radio con velocidad constante. Calcula:
1.tensión del hilo.
2.velocidad de giro.
3.tiempo que tarda en dar una vuelta.
Una masa 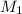 está atada en un extremo de una cuerda de longitud
está atada en un extremo de una cuerda de longitud 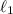 fija por el otro extremo, una segunda masa
fija por el otro extremo, una segunda masa 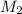 va unidad a la primera mediante otra cuerda de longitud
va unidad a la primera mediante otra cuerda de longitud 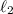 . Ambas se mueven sobre una superficie lisa horizontal con un movimiento circular de periodo
. Ambas se mueven sobre una superficie lisa horizontal con un movimiento circular de periodo 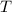 . Determinar la tensión en cada cuerda.
. Determinar la tensión en cada cuerda.
El esquema del sistema se muestra en la figura 1. Sólo nos interesan las fuerzas en la dirección horizontal. Tomamos el criterio de signos habitual, positivo hacia la derecha y negativo hacia la izquierda.
Dado que ambas masas están efectuando un movimiento circular, la fuerza resultante sobre cada una de ellas debe ser igual a la fuerza centrípeta necesaria para mantener dicho movimiento,
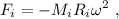
donde
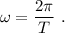
El signo negativo en (1) es necesario ya que, según el diagrama de la figura 1, el centro de giro está a la izquierda, por lo que la fuerza centrípeta debe ir en ese sentido. Ahora ya estamos en condiciones de substituir los datos en (1) para las dos masas,
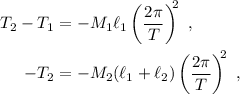
Si sumamos las dos ecuaciones de (3) obtenemos el valor de la tensión de la primera cuerda,
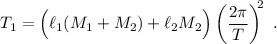
El valor de 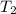 sale directamente de la segunda ecuación de (3),
sale directamente de la segunda ecuación de (3),
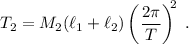


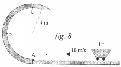

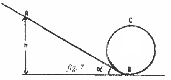
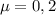 ). La inclinación del plano es de
). La inclinación del plano es de 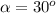 .
.