Problemas de leyes de conservación
El momento angular no necesariamente se conservará:
Recordemos que el momento angular de una partícula se conserva si la fuerza resultante que actúa sobre ella es central (además del caso trivial en que se den las condiciones del principio de inercia). Como en nuestro caso la partícula está sometida únicamente a la fuerza gravitacional, 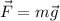 , ésta será central si la intensidad del campo gravitatorio,
, ésta será central si la intensidad del campo gravitatorio, 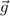 , lo es. Tal será el caso en que éste último sea creado por una sola masa puntual o por una con simetría esférica, pero no en todos los demás (un ejemplo inmediato es el originado por dos masas puntuales).
, lo es. Tal será el caso en que éste último sea creado por una sola masa puntual o por una con simetría esférica, pero no en todos los demás (un ejemplo inmediato es el originado por dos masas puntuales).
La energía mecánica sí se conservará:
La fuerza gravitacional es siempre conservativa, por lo que en una caída libre siempre se satisfacen las condiciones del teorema de conservación de la energía mecánica, independientemente de las características que tenga el campo gravitatorio.
Sobre una superficie horizontal sin fricción se encuentran en reposo 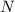 bloques de igual masa,
bloques de igual masa,  , colocados uno al lado del otro en línea recta, separados por una pequeña distancia. Los bloques están numerados de izquierda a derecha, como
, colocados uno al lado del otro en línea recta, separados por una pequeña distancia. Los bloques están numerados de izquierda a derecha, como 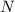 ,
, 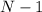 ,
,  ,..., 2, 1. Desde la izquierda incide sobre ellos un bloque de masa
,..., 2, 1. Desde la izquierda incide sobre ellos un bloque de masa 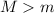 , con velocidad
, con velocidad 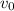 . Suponga que todos los choques son perfectamente elásticos.
. Suponga que todos los choques son perfectamente elásticos.
1.Calcula la velocidad final de cada bloque después de ocurrir todos los choques.
2.Muestra explícitamente (realizando los cálculos antes y después de todos los choques) que se conserva el momento lineal y la energía cinética del sistema.



