Problemas de momento lineal
Sobre un trozo de madera cuya masa de de 20 Kg. hacemos un disparo de fusil. Teniendo en cuenta que en el momento del impacto el proyectil ( m=40g ) lleva una velocidad de 300 m/s y suponiendo que el proyectil quede incrustado en la madera, calcular la velocidad que adquiere el conjunto madera-proyectil y la distancia que recorre el sistema hasta pararse si el coeficiente de rozamiento entre la madera y la superficie horizontal en que se apoya es 0,1.
Un péndulo balístico es un dispositivo que permite determinar la velocidad de un proyectil. Consiste en un bloque grande de madera, de masa M, suspendido verticalmente. Sobre este bloque incide un proyectil, de masa m, a una velocidad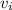 
horizontalmente, de modo que choque y quede incrustado en el bloque de madera. Supongamos que el centro de masa del bloque asciende una altura h después de la colisión. Calcular:
1.La velocidad que llevaba el proyectil.
2.La fracción de energía cinética inicial que se disipa.
Un hombre de 70kg se encuentra sentado sobre una pista de hielo con una escopeta en las manos. Dispara un proyectil de 60g horizontalmente hacia adelante a una velocidad de 1000m/s. ¿Qué distancia resbalará el hombre hacia atrás si el coeficiente de rozamiento dinámico es 0.15?
Dividimos este problema en dos partes:
- Disparo de la bala. Como el disparo es muy rápido, las fuerzas externas no tienen tiempo de actuar. Por lo tanto, en esta fase el momento total del sistema se conserva.
- Deslizamiento hacia atrás. Debido a la velocidad que ha adquirido el hombre, empieza a moverse hacia atrás. El rozamiento se opone a este movimiento, llegando a detenerlo tras recorrer una corta distancia.
Como antes de producirse el lanzamiento, tanto el hombre como la bala dentro de la escopeta están detenidos, la cantidad de movimiento total será cero. Justo después del disparo, pero antes de que el rozamiento tenga tiempo de aparecer, la cantidad de momento seguirá siendo cero, pero ahora tendrá dos contribuciones: el momento de la bala,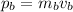 
; y el momento del hombre que retrocede, 
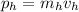. Por lo tanto, la conservación del momento nos proporciona la ecuación
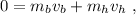
cuya solución es
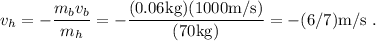
Por lo tanto, el hombre comienza a retroceder a una velocidad de 0.85m/s hacia atrás.
En la segunda fase del problema, el hombre desliza hacia atrás frenado por la fuerza de rozamiento
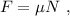
donde N es la fuerza normal de contacto contra el suelo. Como el hombre no atraviesa el hielo, la fuerza normal compensa exactamente su peso,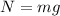 
. Metiendo esto en la segunda ley de Newton,
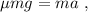
es decir, la aceleración será
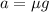
. Debe notarse que hemos puesto signo positivo a la fuerza de fricción ya que el movimiento se realiza hacia atrás: la fuerza de fricción siempre tiene el signo contrario a la velocidad.
Por lo tanto, tenemos un movimiento uniformemente desacelerado, cuyas ecuaciones son
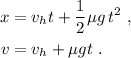
El hombre se detendrá en el momento en que la velocidad sea cero,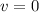 
, lo que nos permite encontrar el tiempo,
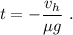
La posición del hombre en este instante se obtiene simplemente substituyendo el valor del tiempo en la ecuación de la trayectoria,
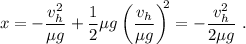
Teniendo en cuenta la ecuación (2) tenemos
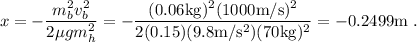
Es decir, el hombre retrocederá un poco menos de 25cm.
