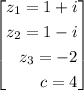Problemas de variable compleja
Se considera la ecuación 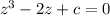 , donde
, donde 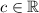 . Hallar el valor de c y las raíces de la ecuación, sabiendo que el afijo de una de ellas está sobre la bisectriz del primer cuadrante.
. Hallar el valor de c y las raíces de la ecuación, sabiendo que el afijo de una de ellas está sobre la bisectriz del primer cuadrante.
Por el teorema fundamental del Álgebra, sabemos que un polinomio de grado n tiene n raíces complejas. Por tanto, llamaremos 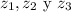 a las tres raíces de esta ecuación.
a las tres raíces de esta ecuación.
Se nos dice que el afijo de una de ellas está situado sobre la bisectriz del primer cuadrante, es decir, la recta 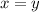 . Por tanto, la parte real y la parte imaginaria de una de las raíces es igual:
. Por tanto, la parte real y la parte imaginaria de una de las raíces es igual:
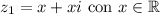
Los coeficientes del polinomio son reales; en consecuencia, el conjugado de 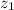 también es raíz:
también es raíz:
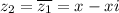
Si dos de las raíces son complejas y el polinomio tiene tres, la tercera raíz será un número real, ya que si fuese complejo su conjugado también lo sería, habiendo 4 raíces en vez de tres. En definitiva:
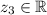
Ahora aplicamos las fórmulas de Cardano-Vieta a este polinomio, con lo que nos queda:
Sustituyendo (1) y (2) en el sistema, este se transforma en:
Lo cual es un sistema con tres incógnitas que no presenta demasiados problemas para ser resuelto. Recordando que un número complejo multiplicado por su conjugado da su módulo al cuadrado (es decir, suma del cuadrado de sus componentes), queda:
Sustituimos, resolvemos y hallamos la solución. Un aviso: en un momento dado nos encontraremos con
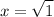
Lo cual nos podría llevar a pensar que x puede ser tanto 1 como -1. Sin embargo, se nos dice que una de las raíces se encuentra en el primer cuadrante; por tanto
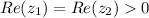
Es decir, x sólo puede valer 1. Resolviendo el sistema, acabamos el problema: