Problemas de análisis en varias dimensiones
Estudiad si 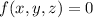 , donde
, donde 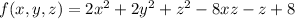 , define la variable
, define la variable  como función implícita de
como función implícita de  y de
y de 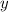 en un entorno del punto
en un entorno del punto 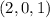 . En caso afirmativo, calculad
. En caso afirmativo, calculad 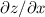 y
y 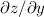 .
.
Sea el cambio de variables dado por
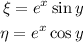
1.Demostrad que el cambio es localmente invertible para todo valor de 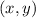
2.Estudiad si, globalmente, el cambio es biyectivo o no
3.Comprovad que
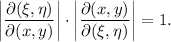
Para que una función sea invertible se tiene que cumplir que sus derivadas parciales sean contínuas y que el determinante de la matriz jacobiana sea diferente de cero en el entorno que la queremos invertir. Esto es lo que nos verifica el teorema de la función inversa para que una función cualquiera sea invertible localmente. Entonces
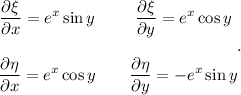
Como podemos comprobar todas son contínuas. Ahora, vamos a calcular el determinante de la jacobiana:
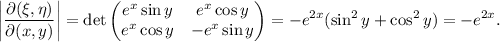
Teniendo en cuenta que 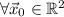 ,
, 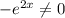 , la función será siempre localmente invertible.
, la función será siempre localmente invertible.
Teniendo en cuenta que en los cambios toman parte funciones trigonométricas, tendremos que a partir de un determinado período la imagen se repetirá y, por lo tanto, la función no será biyectiva globalmente.
Para lograr calcular
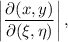
tenemos que expresar 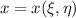 e
e 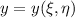 . Hagámoslo
. Hagámoslo
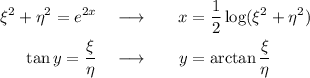
con lo cual
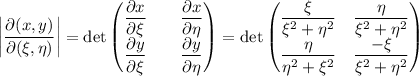
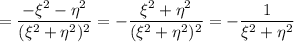
Como hemos visto que 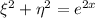 , tenemos que
, tenemos que
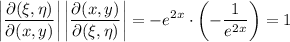
que es lo que queríamos comprobar.


