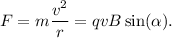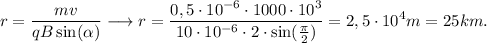¿Con qué radio de curvatura se mueve una partícula con 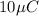 de carga y 0,5mg de masa cuando entra en una región con campo magnético de módulo 2T, perpendicularmente a las líneas de campo, y con una velocidad de 1000Km/s?
de carga y 0,5mg de masa cuando entra en una región con campo magnético de módulo 2T, perpendicularmente a las líneas de campo, y con una velocidad de 1000Km/s?
Tomamos los ejes coordenados de forma que el campo magnético va según el eje OZ, 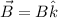 . Según el enunciado, la velocidad es perpendicular al campo magnético, ésta debe estar en el plano OXY, es decir
. Según el enunciado, la velocidad es perpendicular al campo magnético, ésta debe estar en el plano OXY, es decir 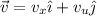 . Para obtener la fuerza magnética total, debemos efectuar el producto vectorial de ambas cantidades, en virtud de la fuerza de Lorentz,
. Para obtener la fuerza magnética total, debemos efectuar el producto vectorial de ambas cantidades, en virtud de la fuerza de Lorentz,
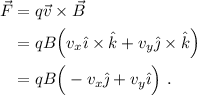
Según la segunda ley de Newton, esta fuerza debe ser igual a la masa por la aceleración, 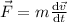 . Esto nos da dos ecuaciones diferenciales acopladas,
. Esto nos da dos ecuaciones diferenciales acopladas,
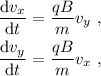
Para resolver este sistema, derivamos respecto al tiempo la primera de las ecuaciones en (2),
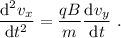
Podemos simplificar el sistema substituyendo las derivadas primeras en (3) según su valor obtenido de (2),
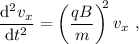
que es la ecuación de un oscilador armónico, cuya solución general es
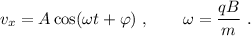
Integrando una vez este resultado, tenemos
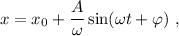
donde 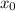 es una constante de integración. Por otra parte,
es una constante de integración. Por otra parte, 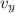 se obtiene directamente (2),
se obtiene directamente (2),
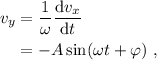
que integrando nos da la coordenada y,
donde 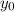 es otra constante de integración (que no tiene por que ser el valor inicial de la coordenada).
es otra constante de integración (que no tiene por que ser el valor inicial de la coordenada).
Como condiciones iniciales, imponemos que la velocidad en el instante inicial es paralela al eje OX, 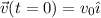 . Substituyendo en (5) y (7), obtenemos
. Substituyendo en (5) y (7), obtenemos

En resumen, la trayectoria de la partícula es
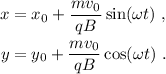
Podemos ver que el movimiento de la partícula es la composición de dos movimientos armónicos, de igual frecuencia y amplitud, en las dos direcciones coordenadas. El resultado de esta composición de movimientos armónicos es un movimiento circular uniforme. Podemos comprobarlo elevando al cuadrado la ecuación (10),
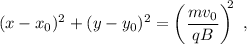
que, en efecto, es la ecuación de una trayectoria circular de radio
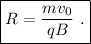

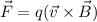 . Esta fuerza es central, ya que siempre es perpendicular a la velocidad. Por tanto, podemos igualar, su módulos con la fuerza centrípeta:
. Esta fuerza es central, ya que siempre es perpendicular a la velocidad. Por tanto, podemos igualar, su módulos con la fuerza centrípeta: