Un protón penetra en una región donde existe un campo magnético uniforme. Explique qué tipo de trayectoria describirá el protón si su velocidad es: a) paralela al campo; b) perpendicular al campo.
1.¿Qué sucede si el protón se abandona en reposo en el campo magnético?
2.¿En qué cambiarían las anteriores respuestas si en lugar de un protón fuera un electrón?
Analizaremos las situaciones según la Ley de Lorentz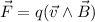 
.
Pregunta a)
En el primer caso, siendo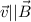 
, el módulo de la fuera se hace 0, ya que 
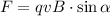siendo 
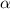el ángulo formado por ambos vectores. Así pues la trayectoria que seguirá el protón en el campo será rectilínea.
Pregunta b)
En el segundo caso, dado que los vectores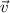 
y 
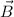son perpendiculares, el módulo del vector fuerza no se anula y su dirección es (de acuerdo con la significación del producto vectorial) perpendicular a ambos vectores. Por tanto, sobre el protón solo actúa una fuerza perpendicular a su velocidad que actuará como fuerza central proporcionando a la partícula un movimiento circular uniforme. El radio se puede obtener igualando la fuerza magnética con la centrípeta,
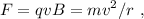
de donde obtenemos
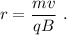
Si el protón es abandonado en reposo, su velocidad es 0. Por tanto sobre él no actúa ninguna fuerza de acuerdo con la Ley de Lorentz. Así pues en este caso la partícula no sufrirá ningún tipo de aceleración y permanecerá en reposo.
Es de notar que la única diferencia que suscita en la Ley de Lorentz el hecho de que la partícula sea un protón o un electrón es el signo de la carga, además del valor de la masa. Así pues el problema se reduce a considerar la diferencia entre
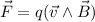
y
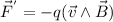
Según las propiedades del producto vectorial, ambos vectores tienen la misma dirección (perpendicular como ya dijimos 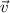a y a 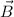), sin embargo difieren en cuanto al sentido, por lo que la fuerza central provocada en el caso b) hará que el electrón gire circularmente en sentido contrario al del protón.
Además, dada la menor masa del electrón, el radio de la trayectoria circular también será menor, como podemos comprobar en la ecuación (2). Este hecho se puede entender mediante el siguiente razonamiento: con menor masa, la fuerza centrípeta necesaria para provocar el mismo giro es menor, por lo que en igualdad de fuerzas -en valor absoluto-, el radio de giro será más pequeño.
