En este caso suponemos que la esfera tiene una densidad volumétrica de carga 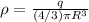. Obviamente la simetría va a ser esférica, por motivos equivalentes a los de la carga puntual. Distinguimos dos regiones: el interior de la esfera y el exterior. En el interior tenemos:

(1)

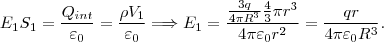
En el exterior tenemos:

(2)

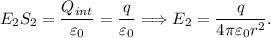
Hay que hacer notar varias cosas en este caso. Cuando nos ponemos en la frontera de las dos regiones (es decir, 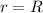) los valores de ambos campos coinciden, como debe ser, ya que no puede haber dos valores distintos para la misma magnitud física en el mismo lugar y tiempo. Otra hecho curioso es que mientras estamos en el interior de la esfera el campo va creciendo linealmente con la distancia al centro, y una vez llegados a la frontera el campo empieza a creer con la inversa del cuadrado de la distancia al centro, ¡del mismo modo que si hubiese una carga puntual en el lugar donde está el centro de la esfera!