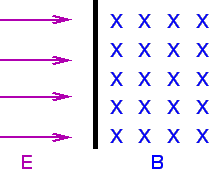
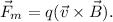En la figura se muestran dos regiones contiguas: a la izquierda está presente un campo eléctrico uniforme (E) en la dirección y sentido mostrados en la figura, y en la derecha un campo magnético uniforme (B) orientado "hacia adentro". La división entre las dos regiones es imaginaria, no hay ningún tipo de barrera.
Dejamos una partícula cargada en reposo en la región izquierda, a una distancia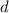 
de la división entre las dos regiones.
1.Expresa la velocidad con la que la partícula llega a la "división" en función de la distancia, el módulo del campo eléctrico y la masa de la partícula.
2.¿Qué trayectoria seguirá la partícula? Justifícalo
3.¿Qué ocurre si dejamos la partícula en reposo ahora en un punto de la región derecha?
La fuerza que experimenta la partícula a causa del campo eléctrico es
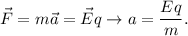
A partir de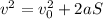 
obtenemos la velocidad final
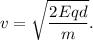
Primero, el campo eléctrico provocará que la partícula se mueva con la aceleración mencionada, hasta llegar a la separación entre medios en un punto A, con una determinada velocidad. Entonces, la fuerza magnética, perpendicular tanto al campo magnético como a la trayectoria de la partícula, ejercerá de fuerza central para la partícula, que describirá una semicircunferencia, hasta llegar otra vez a la separación, ahora en otro punto, B. Por inercia seguirá desplazándose en línea recta hacia la izquierda pero con la deceleración causada por el campo eléctrico, que acabará llevándola otra vez a B. Al volver a entrar en el campo magnético, describirá una semicircunferencia similar, entrando de nuevo al campo eléctrico en un punto C (separado de B la misma distancia que éste está separado de A), y así repitiéndose el proceso.
Al estar la partícula en reposo, no actúa sobre ella ninguna fuerza en un campo magnético, como muestra la fórmula
