Considera un oscilador armónico simple de frecuencia natural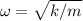 
, el cual se mueve sobre la superficie del suelo, lo que produce una fuerza de rozamiento constante, de valor 
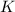. El oscilador comienza, en reposo, separado una distancia 
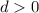de la posición donde la fuerza de recuperación es nula. Calcula cual será la evolución ulterior del oscilador. Considera iguales las fuerzas de fricción estática y dinámica.
Sobre el oscilador se aplican dos fuerzas: la fuerza recuperadora o armónica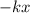 
y la fricción, de valor constante 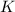y tal que siempre apunta en contra de la dirección donde tiende a moverse el sistema. Aplicando la segunda ley de Newton tenemos
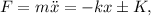
donde se aplica el signo más (superior) si la velocidad tiende a ser negativa, y el signo negativo (inferior) en caso contrario. Por lo tanto, la ecuación diferencial que tenemos que resolver es diferente según si la velocidad del oscilador es positiva o negativa, a saber
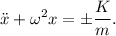
Esta es una ecuación diferencial definida a trozos. No existe ningún método para encontrar una única solución a esta ecuación. El único procedimiento que tenemos es resolver la ecuación igualmente a trozos, considerando tan solo intervalos de tiempo donde la velocidad no cambia de signo, donde la fuerza de rozamiento es constante. En cada intervalo, la solución general de la ecuación (2) es de la forma
donde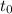 
es el último tiempo en que la velocidad cambió de signo. Como observamos, esta solución corresponden con oscilaciones respecto de un punto de equilibrio diferente del habitual. Sin embargo, la posición de este nuevo punto de equilibrio es diferente según el signo de la velocidad.
Apliquemos, ahora, las condiciones iniciales,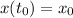 
y 
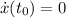, con lo que la solución nos queda
Esta solución será válida hasta el próximo cero de la velocidad, que se dará para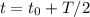 
, siendo 
.
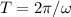Durante el primer semiperiodo (el intervalo de tiempo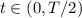 
), la solución es la correspondiente a la ec. (4) con 
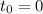y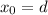 
:
El segundo semiperiodo se puede obtener de la solución general imponiendo las condiciones iniciales que resultan del estado final del semiperiodo anterior,
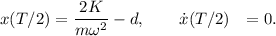
Así, pues, el movimiento durante el segundo semiperiodo es
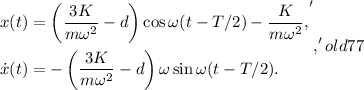
De nuevo, el tercer semiperiodo se iniciará con las condiciones iniciales en que queda el sistema tras el segundo,
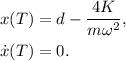
Este proceso se puede repetir de forma indefinida. Podemos encontrar la solución general simplemente observando que, tras cada semiperiodo par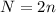 
la posicion final del oscilador es la posición que tenia dos semiciclos antes, habiendo substraído la cantidad 
,
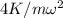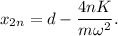
Ésta es, también, la posición inicial para el siguiente semiperiodo (impar), con lo cual tenemos impar,
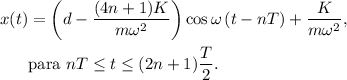
Al final de este semiperiodo impar, la posición es
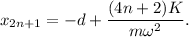
Para encontrar la evolución en el siguiente semiperiodo par tenemos que incrementar el valor de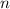 
, lo que equivale a substiuir 
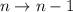en la última expresión. Obtenemos
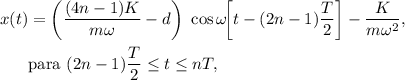
El movimiento será así hasta que, en uno de los cambios de velocidad, la resistencia de la fuerza de fricción sea mayor que la fuerza recuperadora,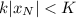 
, lo que impedirá que se inicie la siguiente oscilación. Si esto ocurre tras un semiperiodo impar, se deberá cumplir
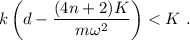
Si esto ocurre tras un semiperiodo par, tendremos
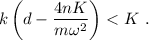
El número de oscilaciones total dependerá de cual de las dos condiciones anteriores se cumpla antes.
