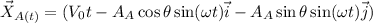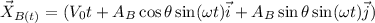Al romperse la cuerda que sujeta dos partículas A y B, el resorte comprimido hace que las partículas se separen . La energía potencial del resorte comprimido es de 27,12 J, y el conjunto inicialmente tiene una velocidad 
=6,096 m/s en la dirección en que se indica en la figura. Si la cuerda se rompe cuando 
= 30°:
a) determinar la velocidad final de cada partícula. cuando el resorte no esta unido a las partículas
b) Si la constante del resorte es k y los extremos del mismo estan unidos a cada partícula describa con ecuaciones el movimiento subsecuente de las mismas.
Peso de A= 8,89 N Peso de B= 13,34 N
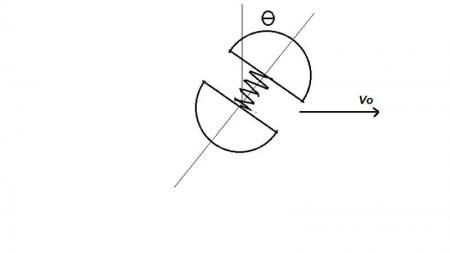
Figura 1. La de arriba es B y la particula de abajo es A (Haz click para ver la imagen a tamaño real)
Considere la gravedad actuando en dirección perpendicular al esquema.
1.Para la primera parte planteo la conservación de la energía, pero incluyo la velocidad de del centro de masas con respecto al sistema de referencia pues la velocidades desarrolladas por cada masa con respecto al centro de masa, son independientes.
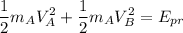
de la conservación de la cantidad de movimiento con respecto al centro de masas
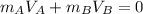
despejando V_A de 2 y reemplazando en 1
por lo que
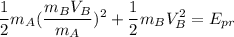
de aqui obtienes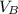 
y si lo reemplazas en 3 obtienes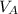 
bien pero ahora sabes que estas velocidades no se desarrollan en la misma dirección que la velocidades del centro de masas 
el esquema no dice cual de las dos partículas es A o B , yo supongo la más pesada B arriba Por lo que la velocidad de la partícula A será
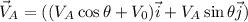
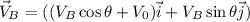
2.para la segunda parte
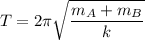
por lo que la frecuencia angular será
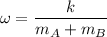
Sabemos que
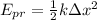
entonces
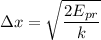
todo se moverá con respecto a un centro de masa que en equilibrio la posición de A será
y la de B
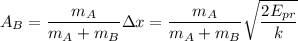
pero como las oscilaciones no siguen exactamente el eje 
ni 
y para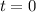 
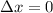
la trayectoria paramétrica de las masas A y B pueden ser escritas entonces como
