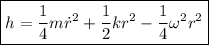Dos partículas de masa 
, unidas mediante un muelle de constante elástica 
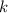y longitud natural despreciable, giran con velocidad angular constante 
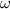con respecto a un eje vertical que pasa por el centro de masas del sistema. Las partículas se mueven sobre un plano horizontal sin rozamiento. Determine:
1.El Lagrangiano del sistema.
2.Las correspondientes ecuaciones de Lagrange.
3.La integral de Jacobi.
Si en reposo la longitud es despreciable, podemos llamar 
a la distancia entre ambas masas (longitud variable del muelle) y si ambas masas son iguales el centro de masas quedara a una distancia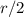 
de ambas (centro geométrico del muelle), y podremos escribir:
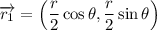
y
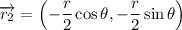
siendo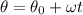 
.
Derivando:
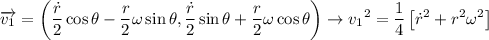
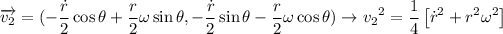
Luego, la energía cinética será:
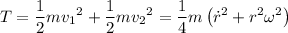
La energía potencial (de tipo elástico) será la que almacene el muelle por el simple hecho de estirarse una distancia , i.e. :
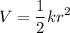
Así, de la definición de Lagrangiana:
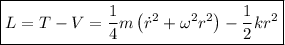
Ahora de las ecuaciones de Lagrange: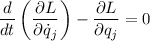 
, identificando 
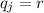como única coordenada generalizada nos queda:
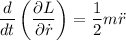
y
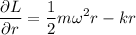
Luego
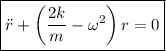
Para la integral de Jacobi, de la definición:
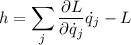
Como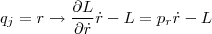 
, quedando:
