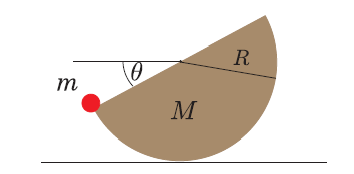
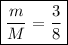Una semiesfera uniforme de masa  y radio
y radio  se encuentra sobre un plano horizontal. Se coloca en su borde (ver figura) una partícula de masa
se encuentra sobre un plano horizontal. Se coloca en su borde (ver figura) una partícula de masa  . Determine mediante el método de los trabajos virtuales la relación entre las masas si en la posición de equilibro
. Determine mediante el método de los trabajos virtuales la relación entre las masas si en la posición de equilibro 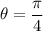 .
.
Podemos identificar 5 fuerzas: los pesos 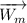 ,
, 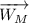 , y la reacción de
, y la reacción de  sobre
sobre  ; la reacción de
; la reacción de  sobre
sobre  , y la reacción del suelo sobre
, y la reacción del suelo sobre  . Estas tres últimas son las llamadas normales (son fuerzas de ligadura), que vemos geométricamente que no realizan trabajo, pues en caso de moverse el punto de apoyo sobre el cual la normal ejerce la fuerza tanto para
. Estas tres últimas son las llamadas normales (son fuerzas de ligadura), que vemos geométricamente que no realizan trabajo, pues en caso de moverse el punto de apoyo sobre el cual la normal ejerce la fuerza tanto para  como par
como par  los desplazamientos virtuales serían perpendiculares a dichas normales.
los desplazamientos virtuales serían perpendiculares a dichas normales.
Del principio de los trabajos virtuales:
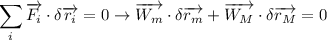
siendo
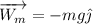
y
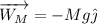
Si elegimos como origen el centro de la esfera:
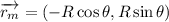
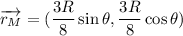
donde el 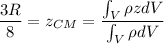 que corresponde a la distancia desde el centro geométrico de la semiesfera considerada como esfera total (nuestro origen) al centro de masas de la semiesfera, si su densidad es constante.
que corresponde a la distancia desde el centro geométrico de la semiesfera considerada como esfera total (nuestro origen) al centro de masas de la semiesfera, si su densidad es constante.
Diferenciando las expresiones anteriores:
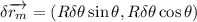
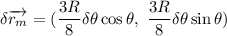
Si introducimos dichos desplazamientos virtuales en la ecuación del principio de trabajos virtuales, queda:
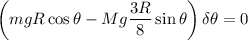
luego
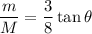
y para 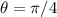 queda:
queda: