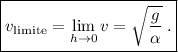Suponemos gotas de lluvia que caen desde una cierta altura 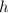 . Si no hubiera fricción, calcular la velocidad con la que llega a tierra. Ahora suponemos que las gotas experimentan una fuerza de fricción
. Si no hubiera fricción, calcular la velocidad con la que llega a tierra. Ahora suponemos que las gotas experimentan una fuerza de fricción 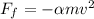 . Calcular
. Calcular 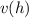 y encontrar la velocidad límite. Para una aplicación realista supondremos los siguientes datos:
y encontrar la velocidad límite. Para una aplicación realista supondremos los siguientes datos: 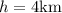 y
y 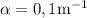 .
.
En primer lugar realizaremos el caso en el que no hay fricción. Para ello utilizaremos la ley de la conservación de la energía, es decir, la energía mecánica inicial es igual a la energía mecánica final
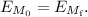
Como la velocidad inicial la supondremos que es nula, la T será 0, eso quiere decir que en el instante inicial las gotas están paradas. Lo mismo con la 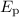 que obtendrá tambien el valor 0, ya que la altura final la consideraremos 0. Quedando la siguiente ecuación
que obtendrá tambien el valor 0, ya que la altura final la consideraremos 0. Quedando la siguiente ecuación
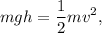
aislando la velocidad final de manera que nos queda
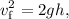
de manera que sustituyendo nos dará
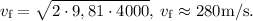
Para el siguiente caso, en que hay fuerza de fricción, aplicamos la segunda ley de Newton, considerando que la únicas fuerzas que actúan en la gota son, su peso y la fuerza de fricción

para ahora hallar 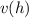 utilizaremos la regla de la cadena
utilizaremos la regla de la cadena
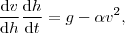
teniendo en cuenta que 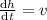 , y desarrollando los siguientes pasos para la integración
, y desarrollando los siguientes pasos para la integración
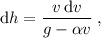
ahora con sus correspondientes limites de integración
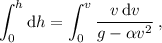
sabiendo que es una integral inmediata del tipo 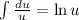 , nos queda
, nos queda
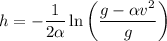
y aislando  en la ecuación de la manera siguiente, obtenemos la velocidad en función de la altura
en la ecuación de la manera siguiente, obtenemos la velocidad en función de la altura
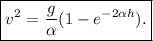
Para encontrar ahora la velocidad límite de la gota, se puede plantear de varias maneras: sabemos que cuando la velocidad es máxima la 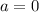 , también razonando que cuando el peso se iguala con la fuerza de fricción, la velocidad es constante
, también razonando que cuando el peso se iguala con la fuerza de fricción, la velocidad es constante 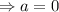 ; de manera que podremos considerar el caso en que la altura tiende a 0
; de manera que podremos considerar el caso en que la altura tiende a 0