Sobre una superficie horizontal sin fricción se encuentran en reposo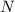 
bloques de igual masa, 
, colocados uno al lado del otro en línea recta, separados por una pequeña distancia. Los bloques están numerados de izquierda a derecha, como , 
, 
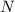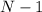,..., 2, 1. Desde la izquierda incide sobre ellos un bloque de masa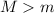 
, con velocidad 
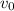. Suponga que todos los choques son perfectamente elásticos.
1.Calcula la velocidad final de cada bloque después de ocurrir todos los choques.
2.Muestra explícitamente (realizando los cálculos antes y después de todos los choques) que se conserva el momento lineal y la energía cinética del sistema.
En este problema aparecen muchos choques entre un bloque que se mueve y otro que está quieto. Así que antes de empezar, estudiaremos este tipo de colisiones en general. Supongamos que el bloque en movimiento tiene una masa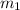 
y su velocidad de incidencia es 
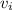. El otro bloque tiene una masa 
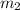. Las masas después de la colisión serán 
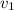y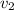 
, respectivamente. Planteando la conservación del momento en este choque genérico
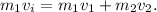
Como el choque es elástico y unidimensional, sabemos que la velocidad de acercamiento (antes del choque) es igual a la velocidad de alejamiento (después del choque),
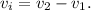
De esta segunda ecuación tenemos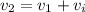 
. Metiendo esto en la primera ecuación,
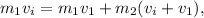
de donde tenemos
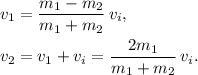
Cuando son los bloques pequeños los que colisionan,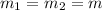 
, de estas ecuaciones queda claro que el bloque incidente queda parado, 
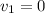, y el bloque que queda quieto sale con la misma velocidad que llevaba el otro antes de golpearle, 
.
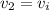Cuando es el bloque grande el que golpea uno pequeño,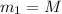 
y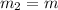 
, entonces la velocidad del bloque grande queda reducida en un factor 
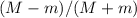. Por su parte, el bloque pequeño se queda una fracción 
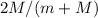de la velocidad del bloque incidente. Notemos como el bloque pequeño después del choque va más rápido que el grande, así que nunca lo vuelve a alcanzar.
Por lo tanto, cuando el bloque grande colisiona con el primer bloque pequeño (el número N) su velocidad se verá reducida. Por su parte, este bloque pequeño avanzará hasta alcanzar el siguiente (el N-1). Al colisionar, el primer bloque se parará (hasta que le vuelva a alcanzar el bloque grande); mientras que el segundo bloque saldrá a la misma velocidad que llevaba el primero. Así dicha velocidad se irá transmitiendo hasta el último bloque, el número 1. Por lo tanto, la velocidad final del primer bloque es
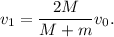
Mientras tanto, recordemos que el bloque N se había parado, así que el bloque grande le volverá a alcanzar. Pero en este momento la velocidad del bloque grande es un factor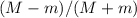 
menor, así que la nueva velocidad después de esta segunda percusión también será menor en la misma proporción. Al final, esta velocidad se transmitirá al último de los bloques pequeños que aún quedan quietos (el número 2, ya que el número 1 había salido disparado a una velocidad mayor y nunca lo alcanzará). Por lo tanto,
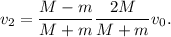
Y así sucesivamente, cada nuevo bloque tendrá un factor 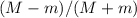más. Así, por lo tanto,
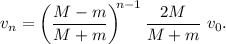
De la misma forma, la velocidad del bloque percutor se habrá reducido en dicho factor un total de N veces, así que
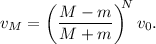
Ahora, para calcular el momento final después de los coches basta con sumar los momentos de cada bloque,
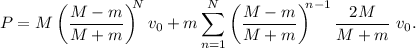
Para hacer ese sumatorio, lo primero que hacemos es un cambio de índice de forma que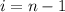 
. Una vez hecho esto, lo que tenemos es una simple serie geométrica incompleta,
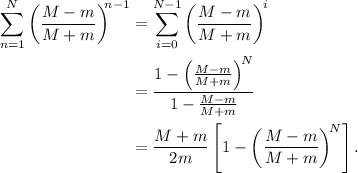
Introduciendo esto en el cálculo del momento,
Los términos con la potencia N se cancelan entre sí, y nos queda únicamente
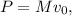
que obviamente es el momento del bloque grande inicialmente, lo cual confirma la conservación del momento (como no podía ser de otra forma, ya que cada colisión individual lo conserva).
Para el cálculo de la energía cinética procedemos de la misma forma. En este caso, calcularemos el doble de la energía cinética, así nos ahorramos el típico factor 1/2,
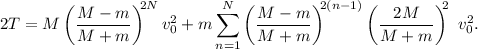
El sumatorio se calcula de forma muy similar,
Metiendo esto en la expresión anterior,
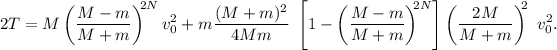
Como antes, se simplifican un montón de cosas y obtenemos
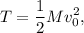
que es justo lo que esperábamos para confirmar la conservación de la energía.
