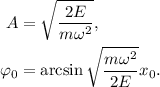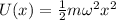La energía total del sistema se puede escribir de la forma

(1)

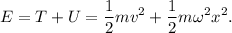
Si aislamos la velocidad, , de la ecuación (1), obtenemos

(2)

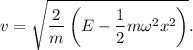
Si tenemos en cuenta que 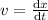, podemos convertir la ecuación (2) en un ecuación diferencial de primer orden separable,

(3)

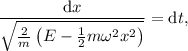
que, dado que la energía es constante (independiente del tiempo) se puede integrar entre el instante inicial, 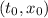, y el final, 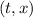, ya que el primer miembro tan solo depende de la posición, , y el segundo tan solo del tiempo, T. Haciendo la integral, pues, obtenemos

(4)

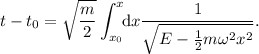
Para poder integrar con mayor facilidad, hacemos el cambio de variable 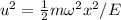, con lo que la integral queda reducida a una primitiva inmediata,

(5)

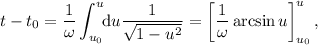
donde 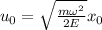. Así, pues,

(6)

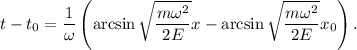
Para encontrar la ecuación del movimiento tan sólo nos queda aislar la variable de esta última ecuación,

(7)

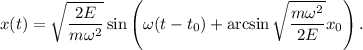
Como vemos, la ecuación (7) tiene la forma de la conocida ecuación del movimiento de un oscilador,

(8)

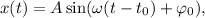
ésto nos permite identificar los parámetros del movimiento, amplitud y fase inicial, en función de las características dinámicas del mismo, energía y posición inicial,

(9)