Sea 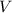 el espacio vectorial de los polinomios reales de grado menor o igual que
el espacio vectorial de los polinomios reales de grado menor o igual que 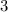 y sea
y sea 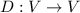 la aplicación derivación, es decir la aplicación definida, para
la aplicación derivación, es decir la aplicación definida, para 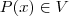 , mediante
, mediante 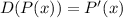 .
.
1.Hallar los autovalores y autovectores de  .
.
2.Sea  la aplicación lineal
la aplicación lineal
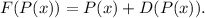
Responder razonadamente si 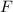 es o no diagonalizable.
es o no diagonalizable.
Problema propuesto en examen final de Álgebra y Geometría, primer curso de Ciencias Físicas, Universidad Autónoma de Madrid. 18 de junio, 1999.
1. Hallar los autovalores y autovector de 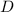 .
.
Para ello, calcularemos en primer lugar la matriz representativa de dicho operador. Para mayor sencillez, tomemos como base, con respecto a la cual calcularemos la matriz representativa del operador, la canónica de 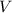 , es decir:
, es decir:
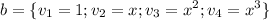
Donde  es una indeterminada cualquiera. Así pues, los transformados de la base son:
es una indeterminada cualquiera. Así pues, los transformados de la base son:

Por tanto, la matriz representativa del operador derivación será:
El polinomio carácterístico será pues:
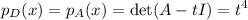
Nótese que aquí 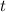 es una indeterminada diferente de la
es una indeterminada diferente de la  del espacio vectorial de los polinomios de grado menor o igual que tres. Se tiene por tanto que el único valor propio del operador es:
del espacio vectorial de los polinomios de grado menor o igual que tres. Se tiene por tanto que el único valor propio del operador es:
La multiplicidad algebraica de este único autovalor será 4, evidentemente.
Calculemos ahora los autovectores correspondientes a este autovalor:
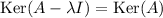
Vemos que en este caso coincide con el núcleo de la aplicación. Por tanto, el espacio de vectores propios estará engendrado por:
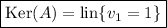
Es decir, el de los polinomios constantes.
2.Responder razonadamente si 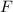 es diagonalizable.
es diagonalizable.
Para resolver este apartado, procederemos de una manera similar al anterior, calculando en primer lugar los transformados de la base canónica de 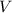 y estudiando posteriormente la matriz representativa del operador. Por tanto:
y estudiando posteriormente la matriz representativa del operador. Por tanto:
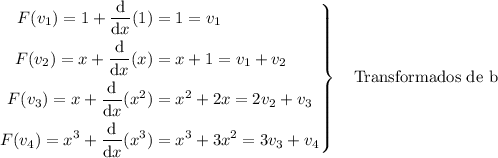
La matriz representativa, por supuesto respecto a 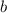 , de
, de 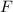 será pues:
será pues:
Análogamente al apartado (1) del problema, el polinomio característico es:

Así pues, el espectro del operador 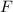 es:
es:
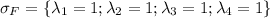
Tenemos que la multiplicidad algebraica del único autovalor del operador es:
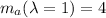
Veamos cuál es su multiplicidad geométrica, recordando que es:
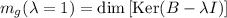
Sea un vector del espacio 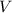 cualquiera:
cualquiera: 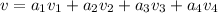 (expresado como combinación lineal de elementos de la base canónica). Entonces:
(expresado como combinación lineal de elementos de la base canónica). Entonces:
Tras resolver el sistema se obtiene que:
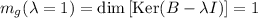
Como las multiplicidades algebraica y geométrica no coinciden:
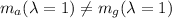
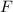 no es diagonalizable, esto es, no existe una base de
no es diagonalizable, esto es, no existe una base de 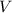 con respecto a la cual la matriz representativa de
con respecto a la cual la matriz representativa de 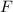 es diagonal.
es diagonal.


