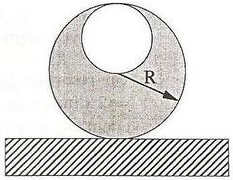
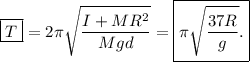Considere un cilindro de radio  y densidad
y densidad 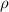 con una perforación cilíndrica de radio
con una perforación cilíndrica de radio 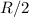 , tal como se muestra en la figura. El cilindro rueda sin resbalar sobre una superficie horizontal realizando pequeñas oscilaciones en torno a su posición de equilibrio. Encuentre el periodo de las oscilaciones.
, tal como se muestra en la figura. El cilindro rueda sin resbalar sobre una superficie horizontal realizando pequeñas oscilaciones en torno a su posición de equilibrio. Encuentre el periodo de las oscilaciones.
Se trata de buscar la energía total del cilindro cuando está en movimiento. Hay: energía cinética de rotación, energía cinética de traslación y energía potencial gravitatoria (la fuerza de rozamiento no realiza trabajo, luego no influye en ningún análisis energético que hagamos).

donde el origen de potenciales se ha tomado a la altura del centro de rotación del objeto, siendo 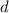 por tanto la distancia entre el centro de masas del objeto y el centro de rotación del objeto. Como rueda sin deslizar,
por tanto la distancia entre el centro de masas del objeto y el centro de rotación del objeto. Como rueda sin deslizar, 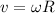 , y por tratarse todas las fuerzas que realizan trabajo en el problema de conservativas,
, y por tratarse todas las fuerzas que realizan trabajo en el problema de conservativas,
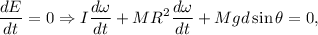
y teniendo en cuenta que 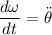 ,
,

ecuación de un oscilador armónico simple, con periodo 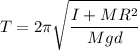 .
.
Sólo resta determinar  ,
, 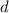 e
e 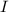 en función de los parámetros del enunciado para calcular el periodo. Con este fin, podemos suponer que el cilindro perforado resulta de la superposición de dos cilindros: uno de radio
en función de los parámetros del enunciado para calcular el periodo. Con este fin, podemos suponer que el cilindro perforado resulta de la superposición de dos cilindros: uno de radio  y densidad
y densidad 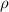 , y otro de radio
, y otro de radio 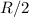 y densidad
y densidad 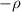 . Esto último es una suposición que nos ayudará a calcular la posición del centro de masa y el momento de inercia; carece de sentido físico ya que equivale a hablar de masas negativas, pero es útil a efectos de cálculo.
. Esto último es una suposición que nos ayudará a calcular la posición del centro de masa y el momento de inercia; carece de sentido físico ya que equivale a hablar de masas negativas, pero es útil a efectos de cálculo.
Situando el origen de coordenadas en el centro de rotación del objeto:
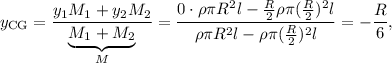
donde 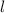 es la longitud de cada cilindro. De esta manera,
es la longitud de cada cilindro. De esta manera, 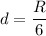 .
.
Para la masa:
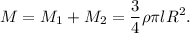
El momento de inercia del cilindro de radio  y densidad
y densidad 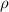 es
es  , y el del cilindro de radio
, y el del cilindro de radio 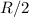 y densidad
y densidad 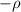 , usando el teorema de Steiner para obtener el momento de inercia en el centro de rotación, resulta ser
, usando el teorema de Steiner para obtener el momento de inercia en el centro de rotación, resulta ser 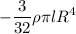 . Así
. Así
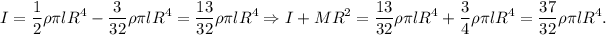
Sustituyendo todo