Una bomba hidráulica de 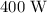 de potencia útil es capaz de extraer el líquido contenido en un depósito con forma semiesférica en
de potencia útil es capaz de extraer el líquido contenido en un depósito con forma semiesférica en 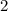 minutos. Determinar la densidad del líquido sabiendo que el radio de la semiesfera es de
minutos. Determinar la densidad del líquido sabiendo que el radio de la semiesfera es de 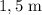 .
.
Problema propuesto en examen de oposiciones a profesor de secundaria, especialidad Física y Química. Castilla-La Mancha, 2002.
Podemos enfocar el problema desde dos puntos de vista:
1) Podemos calcular la posición del centro de masas del depósito, y posteriormente calcular el trabajo necesario para elevar toda la masa concentrada en este punto, desde su posición hasta la parte de arriba.
Por integración, se comprueba que el centro de masas está a una distancia de 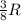 , medida desde el centro de la semiesfera de radio
, medida desde el centro de la semiesfera de radio  . De esta manera, el trabajo requerido para elevar toda la masa
. De esta manera, el trabajo requerido para elevar toda la masa 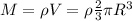 una altura de
una altura de 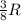 será de
será de
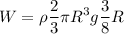
Pero conocemos la relación entre la potencia media, el tiempo empleado y el trabajo:
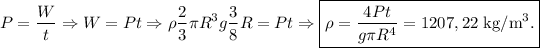
2) De la misma manera, podemos calcular el trabajo (diferencial) necesario para elevar una rebanada de espesor diferencial 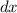 hasta la superficie. Integrando a toda la semiesfera, recuperamos el trabajo realizado para extraer todo el líquido.
hasta la superficie. Integrando a toda la semiesfera, recuperamos el trabajo realizado para extraer todo el líquido.
Una rebanada de espesor diferencial tendrá de masa 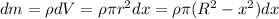 donde se ha usado el Teorema de Pitágoras para relacionar la profundidad a la que está la rebanada,
donde se ha usado el Teorema de Pitágoras para relacionar la profundidad a la que está la rebanada,  , el radio de la semiesfera,
, el radio de la semiesfera,  , y el radio de cada rebanada,
, y el radio de cada rebanada,  . El trabajo elemental será
. El trabajo elemental será 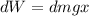 , así que
, así que
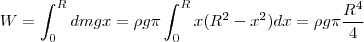
De nuevo, igualando el resultado de (3) con 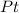 , obtenemos como era de esperar, el mismo resultado simbólico de antes que, al sustituir, da el mismo resultado numérico que antes.
, obtenemos como era de esperar, el mismo resultado simbólico de antes que, al sustituir, da el mismo resultado numérico que antes.


