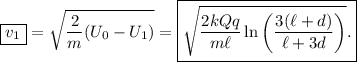Sobre una mesa lisa está sujeta una varilla de longitud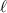 
que tiene una carga 
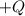uniformemente distribuida. A una distancia 
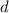de uno de sus extremos se halla una carga puntual 
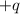de masa 
. El sistema se esquematiza en la figura.
1.Determinar la aceleración inicial de la carga puntual.
2.Obtener la velocidad de la carga puntual cuando ha recorrido una distancia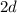 
.
Sabemos que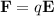 
. Por otra parte, 
, de donde podemos despejar la aceleración. Empezamos calculando el campo eléctrico con la ayuda de la siguiente ecuación
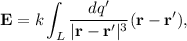
donde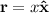 
es el vector de posición del punto donde nos interesa el cálculo (hemos definido el eje 
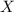a lo largo de la varilla, con su punto más lejos de la carga puntual como el origen), 
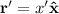el vector de posición de los puntos a integrar de la varilla y 
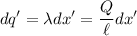. De esta manera,
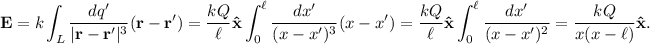
Tal y como hemos definido el sistema de referencia y tal y como pide el enunciado, 
, así que
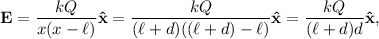
y así
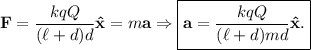
Podemos usar el principio de conservación de la energía mecánica: la fuerza electrostática es la única fuerza que actúa sobre la carga puntual, y ésta es conservativa. Inicialmente, la carga puntual estaba en , a una velocidad nula y tenía una energía potencial eléctrica determinada (que calcularemos en breve), y en el instante final, está en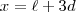 
(ha recorrido 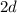) y tiene otra energía potencial eléctrica determinada.
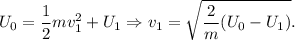
Determinamos en primer lugar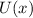 
, tomando el origen de potenciales en el infinito. Sabemos que 
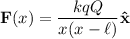, pero 
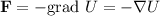, y así
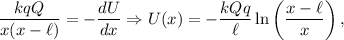
integrando y calculando la constante de integración asignando el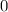 
de potenciales en el infinito.
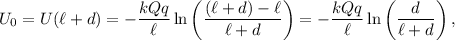
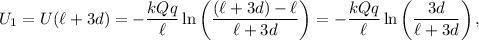
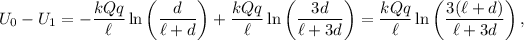
luego
