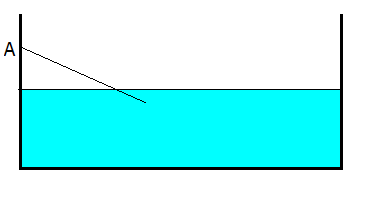
Una barra delgada y homogénea, de longitud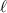 
y de densidad volumétrica de masa 
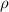, se encuentra sujeta por un extremo de un punto A, mientras que el otro extremo está sumergido en un líquido de densidad 
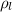. La barra puede moverse libremente alrededor de un eje perpendicular al plano de la figura y que pasa por A. ¿Qué porcentaje de longitud de la barra se halla sumergida, en la posición de equilibrio estable?
El diagrama de fuerzas que actúan sobre la barra se muestra a continuación
donde no hemos tenido en cuenta alguna posible fuerza de reacción en A ya que el objetivo es tomar momentos ahí.
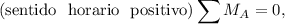
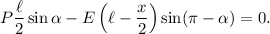
Se tiene que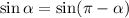 
, que 
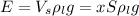, y que 
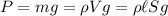, donde 
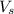es el volumen sumergido, 
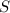es la sección transversal de la barra y 
es la longitud sumergida. Observamos que como la barra es homogénea, el centro de empuje de la parte sumergida coincide con su centro de gravedad. Sustituyendo y simplificando:
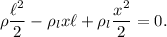
Esto es una ecuación de segundo grado en la incógnita ; sus dos soluciones son:
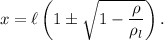
La solución con signo positivo carece de sentido físico ya que sería una longitud mayor que la propia longitud total de la barra 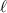. De esta manera, el porcentaje de la barra sumergida será
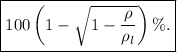
Observamos que por el hecho de ser muy delgada la barra, hemos podido aproximar el volumen de la parte sumergida por directamente la longitud de la parte sumergida por la sección transversal de la barra, en vez de tener que tener en cuenta el ángulo no recto que forma la superficie del líquido con el eje de la barra en el punto de entrada al líquido.
