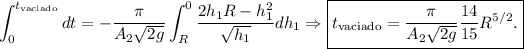Un contenedor semiesférico de radio 
se llena con agua. La parte superior está abierta a la presión atmosférica. En la parte inferior existe un tapón abierto de radio mucho menor que . Halle el tiempo total necesario para vaciar el contenedor. Supóngase que el flujo es ideal.
Suponiendo que el líquido ya ha empezado a descender, y llamando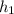 
a la distancia entre el fondo y la altura máxima que alcanza el fluido en el contenedor (por tanto asignando al tapón altura nula), se tiene que la ecuación de Bernoulli toma el siguiente aspecto
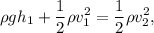
donde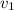 
es la velocidad con la que cambia la altura del fluido en el contenedor y 
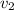es la velocidad con la que sale el fluido por el tapón. Admitiendo a continuación la hipótesis de régimen cuasiestacionario, podemos realizar la aproximación 
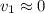, es decir, la altura varía muy lentamente con respecto al tiempo, se tiene que
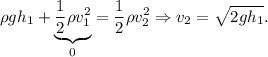
Por otra parte, la ecuación de continuidad aplicada a los puntos de altura 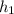y al tapón nos dice que
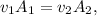
donde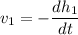 
(el signo negativo se debe a que la altura disminuye con el tiempo), 
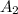es el área del tapón, 
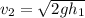como ya hemos obtenido antes, y 
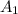es el área que cubre el fluido a altura 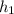. Como sabemos que el fluido está contenido en un contenedor semiesférico, el área 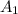será una función del tipo 
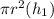, donde se puede comprobar que 
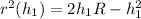. Luego 
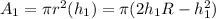y obtenemos la siguiente ecuación diferencial
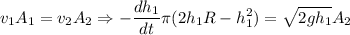
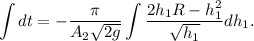
En el instante inicial, la altura era el radio de la semiesfera, y en el instante de vaciado total, la altura es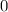 
, por tanto
