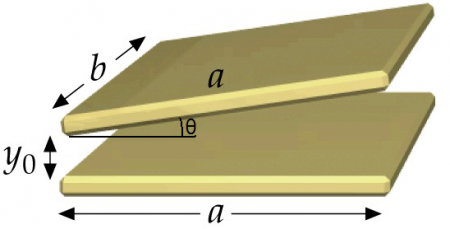
Determine la capacidad de un condensador formado por dos placas planas de longitud  y anchura
y anchura 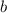 , cuyos planos forman un ángulo
, cuyos planos forman un ángulo 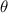 muy pequeño, siendo la distancia mínima que los separa
muy pequeño, siendo la distancia mínima que los separa 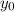 .
.
Este problema pone de manifiesto cómo usar un resultado elemental para resolver un problema algo complicado. Sabemos por cualquier libro de Física General que la capacidad de un condensador de placas planas y paralelas es
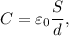
donde 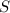 es la superficie de las placas y
es la superficie de las placas y 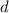 es la distancia que las separa.
es la distancia que las separa.
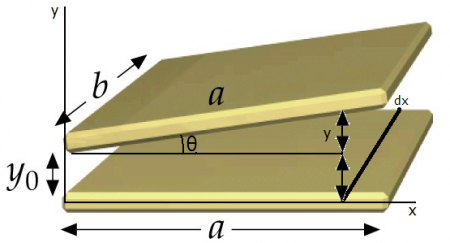
A la vista de la siguiente figura
podemos dividir el condensador en condensadores infinitesimalmente pequeños de superficie 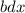 y distancia
y distancia 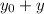 , donde por trigonometría,
, donde por trigonometría, 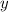 resulta ser
resulta ser 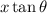 . La capacidad de cada uno de estos condensadores infinitesimales resulta ser
. La capacidad de cada uno de estos condensadores infinitesimales resulta ser
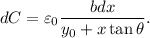
Al ser conductores en equilibrio electrostático, la diferencia de potencial entre las dos placas es constante, luego todos los condensadores infinitesimales están sometidos a la misma diferencia de potential entre sus correspondientes placas. Podemos por tanto suponer que están en paralelo, y la capacidad equivalente será la suma de todas estas capacidades infinitesimales: una integral definida.
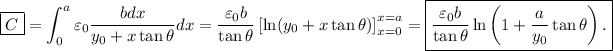
Observamos que se ha podido usar la capacidad de un condensador de láminas planas y paralelas sólo porque el ángulo 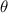 es muy pequeño y por tanto las placas son aproximadamente paralelas. Asímismo, en el límite
es muy pequeño y por tanto las placas son aproximadamente paralelas. Asímismo, en el límite  debemos tener que la capacidad se reduce a
debemos tener que la capacidad se reduce a 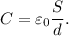 Veamos si es cierto:
Veamos si es cierto:
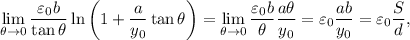
donde se han usado los infinitésimos equivalentes
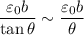
y
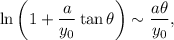
ambos válidos para  .
.