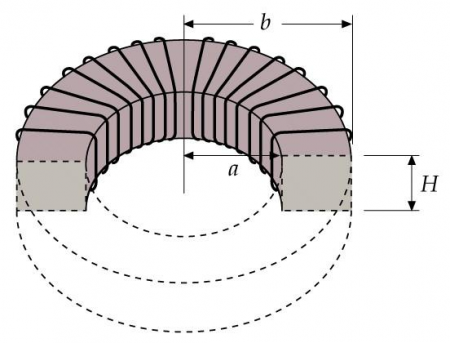
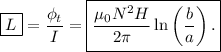Calcule la inductancia de un toroide de sección rectangular como el que se muestra en la siguiente figura
en función de 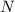 (el número total de vueltas),
(el número total de vueltas),  (el radio interior),
(el radio interior), 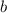 (el radio exterior), y
(el radio exterior), y 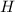 (la altura del toroide).
(la altura del toroide).
En cualquier libro de Física General se demuestra (con la Ley de Ampère) que la inducción magnética creada por un toroide se manifiesta en el interior del mismo, y además es tangente a cualquier circunferencia centrada en el centro del toroide y contenida en el plano de éste, con valor
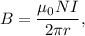
donde 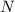 es el número de vueltas,
es el número de vueltas, 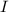 la intensidad y
la intensidad y  el radio medido desde el centro del toroide (en nuestro caso
el radio medido desde el centro del toroide (en nuestro caso 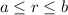 ).
).
La resolución del problema consistirá en la aplicación de la relación 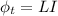 , de donde se despejará
, de donde se despejará 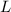 (coeficiente de autoinducción o inductancia) tras calcularse
(coeficiente de autoinducción o inductancia) tras calcularse 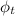 (el flujo magnético através del toroide).
(el flujo magnético através del toroide).
El flujo magnético através de una de las 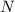 espiras cuadradas (tomando un elemento diferencial de área de anchura
espiras cuadradas (tomando un elemento diferencial de área de anchura 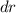 y altura
y altura 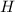 ) del toroide será
) del toroide será
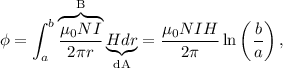
ya que 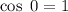 , al ser
, al ser 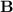 perpendicular al plano de la espira, ya que
perpendicular al plano de la espira, ya que 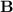 también es tangente a cualquier circunferencia centrada en el centro del toroide y contenida en el plano de éste, como ya se ha dicho.
también es tangente a cualquier circunferencia centrada en el centro del toroide y contenida en el plano de éste, como ya se ha dicho.
Esto es el flujo através de una de las 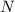 espiras. El flujo através de todo el toroide será
espiras. El flujo através de todo el toroide será
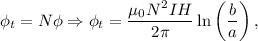
y entonces