Una esfera dieléctrica de radio  está polarizada uniformemente según un vector de polarización
está polarizada uniformemente según un vector de polarización 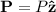 . Determinar el vector
. Determinar el vector 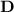 y el vector
y el vector 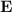 en el centro de la esfera.
en el centro de la esfera.
La filosofía de la resolución del problema consistirá en obtener las densidades de carga ligada e integrar éstas para obtener el campo electrostático, y luego usar la relación entre el desplazamiento eléctrico y la polarización para despejar 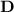 .
.
Tenemos que 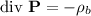 y
y 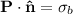 . Como
. Como 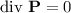 , no hay densidad volumétrica de carga ligada, y en coordenadas esféricas,
, no hay densidad volumétrica de carga ligada, y en coordenadas esféricas, 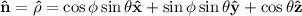 . De esta manera,
. De esta manera, 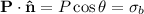 , y tenemos que calcular el campo electrostático debido a esta distribución de carga superficial.
, y tenemos que calcular el campo electrostático debido a esta distribución de carga superficial.
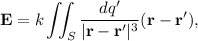
donde 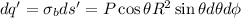 , donde se ha expresado el elemento diferencial de superficie en coordenadas esféricas. Se tiene además que
, donde se ha expresado el elemento diferencial de superficie en coordenadas esféricas. Se tiene además que 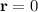 (nos interesa el campo en el centro de la esfera) y
(nos interesa el campo en el centro de la esfera) y 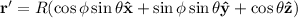 . Sustituyendo tenemos que
. Sustituyendo tenemos que
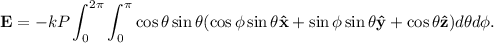
Las integrales en 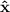 y
y 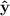 son funciones del tipo
son funciones del tipo 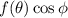 y
y 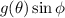 respectivamente, y de esta manera las integrales con respecto a
respectivamente, y de esta manera las integrales con respecto a 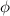 entre
entre 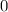 y
y 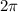 son
son 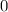 . Por tanto sólo hay campo en
. Por tanto sólo hay campo en 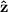 :
:
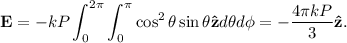
En el SI, 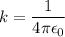 , así que
, así que
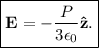
Sabemos además que 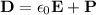 , lo que nos permite concluir que
, lo que nos permite concluir que
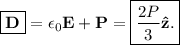
Se puede demostrar además que este es el valor del campo electrostático en toda la esfera dieléctrica (por tanto el vector desplazamiento eléctrico también toma el valor constante calculado en este problema). El lector interesado tiene la demostración en Introduction to Electrodynamics de Griffiths.


