1
Nivel
Primer ciclo
Dificultad
5
Categoría
Física cuántica
La función de onda del oscilador armónico en 1D es
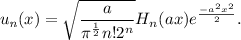
(1)
donde 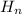 son los polinomios de Hermite. Demostrar que para
son los polinomios de Hermite. Demostrar que para 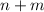 impar,
impar,
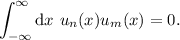
(2)
Solución disponible
H[e]rtz
Primero comprovaremos la ortonormalidad de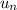 y
y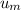
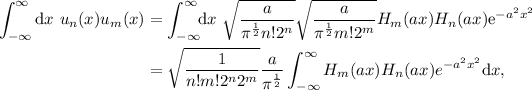
(1)
Sabemos que los polinomios de Hermite tienen la siguiente propiedad,
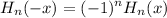
(2)
entonces
[ERROR DE LaTeX. Error: 4 ]
(3)
Ahora nos fijamos en la segunda integral, y hacemos el cambio de variable
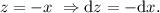
(4)
entonces queda
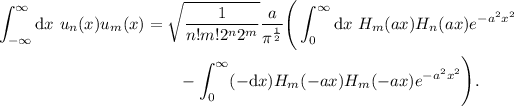
(5)
aplicamos (2)
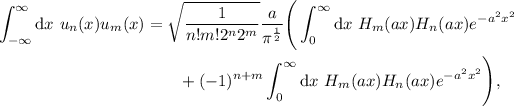
(6)
aplicando la condición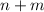 impar, que implica
impar, que implica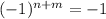 ,
,
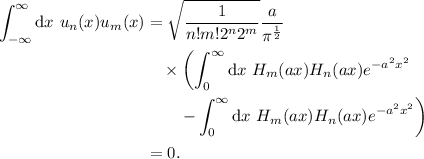
(7)


