Paso 1. Comenzamos la demostración comprobando el primer caso posible, 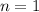. Como 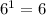termina en seis, el primer caso es correcto.

Paso 2. Por hipótesis de inducción, suponemos que la proposición es válida para un 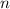arbitrario. Que termine en 6 significa que existe un número entero, 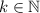, tal que

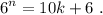
(1)

Paso 3. Haciendo uso de (1), debemos demostrar que la proposición también es cierta para el siguiente número natural, 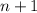. Es decir, debe existir un número natural 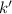tal que

(2)

Partimos multiplicando por 6 la ecuación (1),

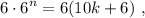
(3)

simplificando,

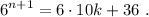
(4)

Podemos descomponer el 36 como 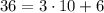, con lo que tenemos

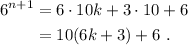
(5)

Comparando con (2) vemos que se debe cumplir 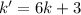. Por las propiedades de multiplicación y suma de números naturales, 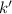es un número natural. Esto completa la demostración.