Demostrar, aplicando el teorema de conservación de la energía mecánica, que si lanzamos un cuerpo A verticalmente hacia arriba con velocidad triple que otro B, la altura alcanzada por A es nueve veces la de B.
Según el teorema de conservación de la energía mecánica, si sobre un sistema solamente actúan fuerzas conservativas, entonces la suma de la energía cinética más la potencial del sistema no varía, en otras palabras, la energía mecánica de un sistema permanece constante si las fuerzas que actúan sobre él son conservativas.
Al lanzar un cuerpo hacia arriba, únicamente actúa la fuerza gravitatoria, que es conservativa; suponiendo que no hay rozamiento con el aire, podemos decir que en el momento del lanzamiento el cuerpo tiene solamente energía cinética, y al aumentar la altura, progresivamente esta energía cinética se irá transformando en energía potencial. Como la energía mecánica (suma de la cinética y potencial) se conserva, entonces, podemos escribir que:
[ERROR DE LaTeX. Error: 4 ]
Siendo [ERROR DE LaTeX. Error: 4 ] la energía mecánica del cuerpo antes del lanzamiento y la energía mecánica cuando éste alcanza la altura máxima, respectivamente. Por tanto, la altura alcanzada será:
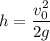
Para el caso particular del cuerpo A y B:
[ERROR DE LaTeX. Error: 4 ]
[ERROR DE LaTeX. Error: 4 ]
Si dividimos miembro a miembro cada expresión, obtenemos que:
[ERROR DE LaTeX. Error: 4 ]
Concluimos que la altura alcanzada por el cuerpo A es:
[ERROR DE LaTeX. Error: 4 ]
[ERROR DE LaTeX. Error: 4 ]


