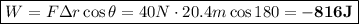Un cuerpo de masa 2 kg desciende en caída libre. Toma 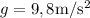 .
.
1.¿Qué fuerza constante es necesario aplicarle en el instante en que su velocidad es de 20,4 m/s para detenerlo en 2 s?
2.¿Qué trabajo se realiza sobre el cuerpo desde que se aplica la fuerza hasta que se detiene?
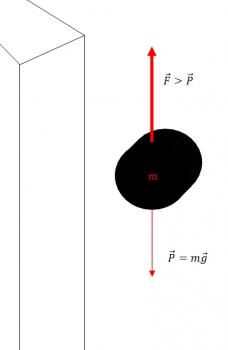
En primer lugar, hemos de tener en cuenta que si el cuerpo desciende en caída libre, se debe a que sobre él actúa únicamente la fuerza peso que provoca que su velocidad vaya en aumento, es decir, es un movimiento acelerado.
Para responder a la primera pregunta, si queremos que se detenga a los 2 segundos en un instante en el que tiene una velocidad determinada, debemos aplicarle una fuerza hacia arriba, es decir, en sentido contrario, y mayor que el peso, con el fin de que el cuerpo experimente una aceleración ''negativa'' que lo haga deternerse; a continuación se muestra la situación:
Podemos calcular esta aceleración teniendo en cuenta que ésta se define como la rapidez con que cambia la velocidad, es decir:
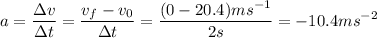
Para calcular la fuerza resultante que provoque esta aceleración, aplicamos la segunda ley de Newton, según la cual, el cambio del momento lineal de un cuerpo es proporcional a la fuerza que actúa y se produce en la dirección de dicha fuerza. Expresado matemáticamente:
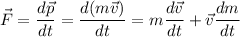
Como la masa permanece constante, el segundo sumano de la expresión anterior será cero, con lo que se obtiene la expresión básica de esta ley:
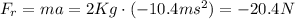
Como ya se ha dicho, esta fuerza ha de estar dirigida hacia arriba. Ahora bien, esta no es la fuerza que hemos de aplicar al cuerpo para que se detenga a los 2s cuando tiene una velocidad de 20.04m/s, pues:
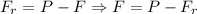
Por tanto, la fuerza que hay que aplicarle es:
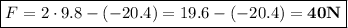
Por otro lado, el trabajo mecánico realizado por la fuerza constante 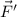 que actúa sobre el cuerpo que realiza el desplazamiento
que actúa sobre el cuerpo que realiza el desplazamiento 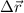 es igual al producto escalar entre la fuerza y el desplazamiento, es decir:
es igual al producto escalar entre la fuerza y el desplazamiento, es decir:
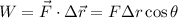
Ahora bien, ¿cuál es ese desplazamiento?
Al tratarse de un movimiento uniformemente variado la ecuación general de la posición que lo representa es:
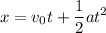
El desplazamiento es la variación de posición neta, es decir: 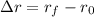 . Considerando en este caso que
. Considerando en este caso que 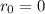 , entonces:
, entonces:
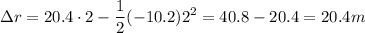
Por otro lado, como se observa en el dibujo, la fuerza actúa en sentido contrario a la dirección del desplazamiento, por lo que el trabajo realizado por la fuerza es negativo, pues se opone al desplazamiento. Por tanto: