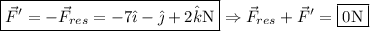Dadas las fuerzas siguientes: 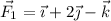 ,
, 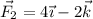 ,
, 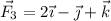 , calcular:
, calcular:
1.La fuerza resultante.
2.Su módulo.
3.Ángulos que forma la fuerza resultante con los ejes cartesianos.
4.Vector unitario de la misma.
5.La fuerza adicional que hay que aplicar para que la nueva resultante sea nula.
1. Para calcular la fuerza resultante, no tenemos más que hacer la suma vectorial de las fuerzas dadas. Así pues:
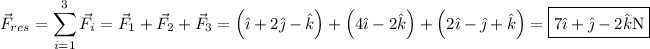
2. El módulo de la fuerza resultante, será por tanto:
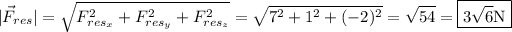
3. Para hallar los ángulos que forma la fuerza resultante con los ejes cartesianos, podemos hallar los cosenos directores. En una base ortonormal, (estamos trabajando con la denominada base canónica),se llaman cosenos directores de un vector a los cosenos de los ángulos que forma el vector con los vectores de la base. Por tanto, una vez obtenidos dichos cosenos, podemos hallar el ángulo:
Cabe destacar que se ha de verificar que:
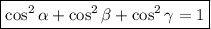
4. Lo primero que hemos de tener claro es que un vector unitario tiene de módulo la unidad. Así pues, la normalización de un vector consiste en asociarle otro vector unitario, de la misma dirección y sentido que el vector dado, dividiendo cada componente del vector por su módulo. Por tanto, un vector unitario de la fuerza resultante será:
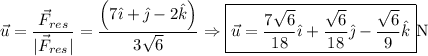
5.La fuerza adicional que hay que aplicar para que la nueva resultante sea nula es justamente: 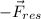 . Por tanto:
. Por tanto: