Mercurio describe una órbita elíptica alrededor del Sol. En el afelio su distancia al sol es de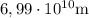 
y su velocidad orbital 
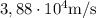, siendo su distancia al Sol en el perihelio de 
.
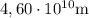1.Calcule la velocidad orbital de Mercurio en el perihelio.
2.Calcule las energías cinética, potencial y mecánica de Mercurio en el perihelio.
3.Calcule el módulo de su momento lineal y su momento angular en el perihelio.
4.De las magnitudes calculadas en los apartados anteriores, decir cuáles son iguales en el afelio.
Datos:
- Masa de mercurio:
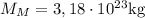, - Masa del Sol
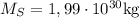, - Cte. de Gravitación Universal
.
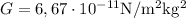En primer lugar debemos hacernos un esquema de la situación dinámica del planeta. Sobre él se ejerce solamente una fuerza, la fuerza gravitatoria que actúa, además, como fuerza centrípeta, por tanto, y al ser ésta una fuerza central podemos aplicar el Principio de Conservación del momento angular
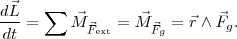
Por tanto, y desarrollando
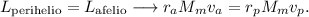
De donde concluimos que
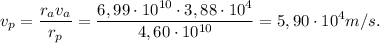
Sean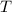 
y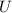 
las energías cinética y potencial respectivamente y 
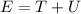la energía mecánica. Entonces
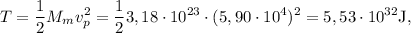
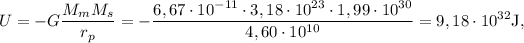
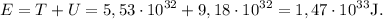
El módulo del momento lineal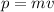 
referido al perihelio es
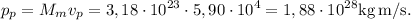
El módulo del momento angular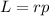 
en la misma posición es
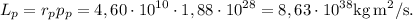
Son constantes, únicamente, el momento angular y la energía mecánica.
