Para despegar, dos planeadores se arrastran uno tras el otro mediante un avión de
transporte. La masa de cada planeador es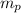 
y la fuerza con que se oponen al arrastre es
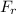. Los cables empleados para unir los tres aviones no deben someterse a tensiones
superiores a 
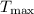. ¿Cuál es la aceleración máxima con que puede arrastrar los
planeadores sin que se rompan los cables? ¿Cuál es la longitud mínima de pista
requerida, si es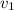 
la velocidad de despegue?
Tenemos dos cables: el que une el avión tractor y el primer planeador, con una tensión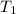 
; y el que une los dos planeadores, sometido a una tensión 
.
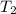Aplicamos la segunda ley de Newton a las fuerzas aplicadas sobre cada planeador;
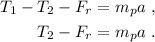
Restando las dos ecuaciones llegamos a
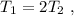
es decir, la tensión del primer cable es mayor que la del segundo (lógicamente, ya que el primero arrastra los dos planeadores). Es decir, el cable que corre mayor riesgo de romperse es el primero. En el límite, tendremos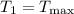 
.
Sumando las dos ecuaciones de (1) llegamos a
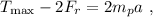
y por lo tanto la máxima aceleración será
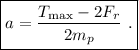
A esta aceleración, el tiempo necesario para alcanzar la velocidad de despegue será
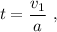
durante este tiempo, los planeadores habrán recorrido una distancia
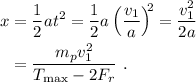
Por lo tanto, la longitud de la pista debe ser, por lo menos, igual a esta distancia.
