Apartado 1

Estamos ante un tiro parabólico completo,resultante de uno de avance horizontal, rectilíneo y uniforme, y otro rectilí- neo y uniformemente acelerado; por tanto las ecuaciones según OX serán:

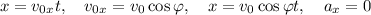
La aceleración en este caso es cero, de ahí que sea un movimiento uniforme. Por otro lado, las ecuaciones del movimiento en el eje OY son:

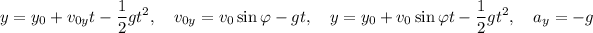
Por tanto, las ecuaciones del movimiento del cuerpo serán:

[ERROR DE LaTeX. Error: 4 ]

[ERROR DE LaTeX. Error: 4 ]

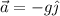
Cuando el cuerpo alcanza el suelo, 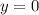luego:

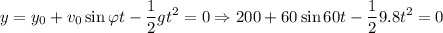
Tras resolver la ecuación de segundo grado, se obtienen dos valores para el tiempo:

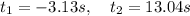
El tiempo que tarda en alcanzar el suelo es por tanto 13.04s aproximadamente, ya que la segunda solución de la ecuación cuadrática no tiene significado físico. Por tanto, la velocidad con la que llega al suelo es:

Apartado 2

En lo que respecta al alcance total, es la distancia desde el lugar en el que se lanzó el cuerpo al punto en que el cuerpo pasa por la misma horizontal de aquél. En realidad ya lo hemos hemos hecho, al hacer que 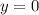. De todos modos, hay una expresión para calcular el alcance total a la que podemos llegar de la siguiente forma:

En la ecuación del movimiento, despejamos el tiempo, teniendo en cueta que hay una altura inicial:

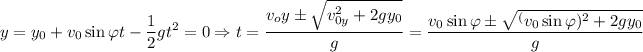
Para hallar el alcance máximo o total, simplemente multiplicamos este valor por:

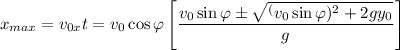
El resultado al que se llega es el siguiente:

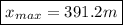
Lógicamente tomando el valor del tiempo con significado físico, es decir, no el valor negativo.