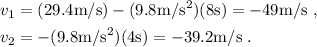Desde un punto situado a una altura h, se lanza verticalmente una piedra hacia arriba con una velocidad de 29,4 m/s. Desde el mismo punto se deja caer otra piedra, 4 s después de lanzar la primera. Calcula:
1.¿En qué instante y en qué lugar alcanza la primera piedra a la segunda?
2.¿Qué velocidad tiene cada una de ellas en ese instante?
Para empezar, escribimos las ecuaciones del movimiento de cada piedra. En ambos casos, la altura inicial es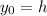 
, y la aceleración es la de la gravedad 
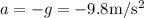. La primera piedra se lanza con una velocidad inicial 
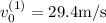, mientras que la segunda se deja caer, es decir, sale de parado 
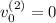. La segunda piedra, además, parte un tiempo 
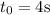más tarde, por lo que será necesario reemplazar el tiempo, t, por 
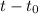. En resumen, tenemos
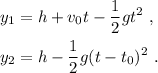
La primera piedra alcanza a la segunda en el instante en que se ambas se encuentren en la misma posición,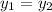 
, lo cual nos da una ecuación
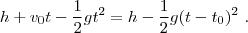
Procedemos a desarrollar y simplificar la ecuación,
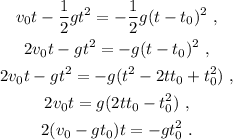
Por lo tanto, podemos aislar el tiempo para obtener
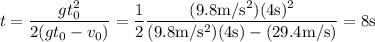
Para saber la posición, basta con substituir este tiempo en cualquiera de las dos ecuaciones del movimiento (1), el resultado será el mismo para las dos (ya que precisamente hemos impuesto esa condición). Por ejemplo, probemos con la ecuación de la segunda piedra,
Es decir, las piedras se encuentran 78.4m por debajo del punto de partida.
La ecuación de la velocidad para cada partícula se obtiene substituyendo en la fórmula típica del movimiento rectilíneo uniformemente acelerado (o derivando la ecuación (1), si ya hemos aprendido esta técnica),
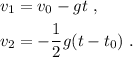
Ya podemos proceder a substituir los datos,
