na partícula está animada de una velocidad de componentes:
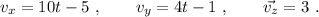
Si su vector posición para 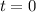 es
es 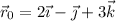 , calcula:
, calcula:
1.Aceleración a los 3 s.
2.Desplazamiento entre 2 y 3 s.
3.Componentes intrínsecas de la aceleración.
Apartado 1
La aceleración se define como la rapidez con que cambia la velocidad, es decir:
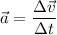
Ahora bien, si medimos la aceleración en intervalos de tiempo muy cortos, la aceleración media pasa a ser aceleración instantánea. Para ello:
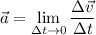
Esta expresión es justamente la de la derivada de la velocidad con respecto al tiempo. Por tanto, como conocemos las componentes de la velocidad, la aceleración instantánea se obtiene derivando esta velocidad con respecto al tiempo, es decir:
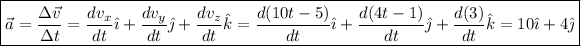
Observamos que la aceleración no depende del tiempo, es decir,  . Luego a los tres segundos, y en cualquier instante, la aceleración será: [ERROR DE LaTeX. Error: 4 ] y el módulo de ésta será:
. Luego a los tres segundos, y en cualquier instante, la aceleración será: [ERROR DE LaTeX. Error: 4 ] y el módulo de ésta será:
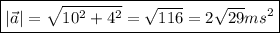
Apartado 2
El desplazamiento es la variación de posición neta, por lo que en primer lugar es necesario calcular el vector posición. Para ello, hemos de tener en cuenta que:
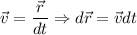
Por tanto, para calcular el vector posición hemos de integrar:
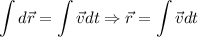
Podemos expresar este vector integral en función de sus componentes coordenadas, en este caso las componentes de la velocidad:
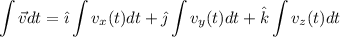
Por tanto:
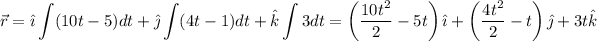
Ahora bien, esta integral es indefinida, luego existen infinitas primitivas que se diferencian entre sí en una constante de integración 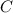 . Simplificando y añadiendo la constante, el vector posición queda:
. Simplificando y añadiendo la constante, el vector posición queda:
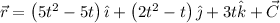
¿Cuál es entonces esa constante? Podemos calcularla, pues conocemos el vector posición en un instante determinado: 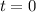 . Por tanto:
. Por tanto:
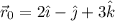
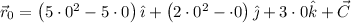
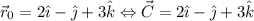
Por tanto, el vector posición será:
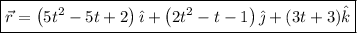
El desplazamiento efectuado entre 2 y 3s será: 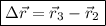
[ERROR DE LaTeX. Error: 4 ]-[ERROR DE LaTeX. Error: 4 ]
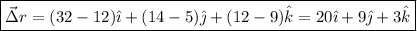
Apartado 3
Podemos distinguir dos ''tipos'' de aceleración, la tangencial y la centrípeta o normal. Estos son los que suelen denominarse componentes intrínsecas de la aceleración, ya que el sistema de referencia en el que se definen es propio o intrínseco a la trayectoria, pues pueden definirse en cualquier punto de la misma en el que se encuentre el móvil.
En primer lugar, calculamos la aceleración tangencial, que es la que produce cambios en el módulo de la velocidad:
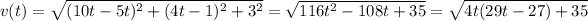
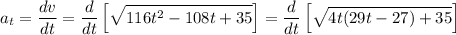
Derivando con respecto al tiempo obtenemos la aceleración tangencial:
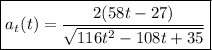
En notación vectorial sería:
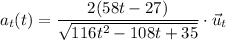
Donde 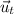 es un vector unitario en la dirección tangencial.
es un vector unitario en la dirección tangencial.
Por otro lado, la aceleración centrípeta o normal, aparece cuando los movimientos son curvilíneos y produce cambios en la dirección de la velocidad sin afectar a su módulo. Como las dos componentes intrínsecas son perpendiculares, la aceleración total será:
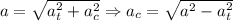
Por tanto el módulo de la aceleración centrípeta o normal, en función del tiempo, será:
[ERROR DE LaTeX. Error: 4 ]
Operando, obtenemos finalmente la aceleración normal:
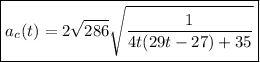
En notación vectorial, diremos que la aceleración centrípeta es:
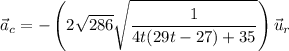
Donde 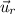 es el vector unitario en la dirección radial. Además, el signo negativo indica que está dirigida hacia el centro (tomando como origen de referencia el centro de la curva).
es el vector unitario en la dirección radial. Además, el signo negativo indica que está dirigida hacia el centro (tomando como origen de referencia el centro de la curva).
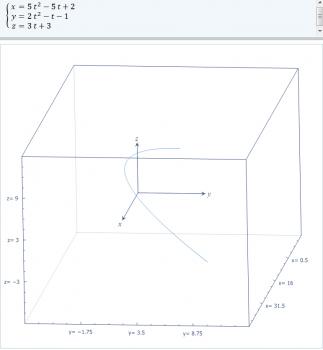
Podemos comprobar que se trata de un movimiento curvilíneo al tener las ecuaciones paramétricas del movimiento del cuerpo:
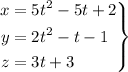
Si lo representamos gráficamente, se observa que el cuerpo sigue una trayectoria curvilínea: