Usa la integración de Romberg para evaluar la integral de 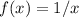 entre
entre 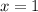 y
y 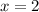 . Lleva seis decimales y continúa hasta que no haya cambio en la quinta cifra decimal. Compara con el valor analítico,
. Lleva seis decimales y continúa hasta que no haya cambio en la quinta cifra decimal. Compara con el valor analítico, 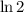 .
.
La integración de Romberg se basa en el uso de la regla del trapecio compuesto, el cual se usa para obtener aproximaciones preliminares. Con el proceso de extrapolación de Richardson se mejoran dichas aproximaciones. Si 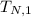 es la aproximación calculada de la integral
es la aproximación calculada de la integral 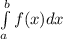 por medio de la regla trapezoidal con
por medio de la regla trapezoidal con 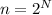 subintervalos, tenemos la siguiente relación de recurrencia que nos va a permitir calcular dicha aproximación:
subintervalos, tenemos la siguiente relación de recurrencia que nos va a permitir calcular dicha aproximación:
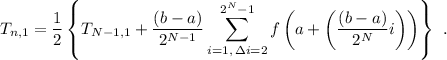
Los restantes términos de las distintas sucesines se calculan mediante la fórmula general de extrapolación de Romberg:
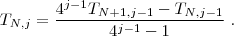
A continuación se presenta la tabla con los valores calculados para los  mediante (1) y (2):
mediante (1) y (2):
| N | j = 1 | j = 2 | j = 3 | j = 4 |
|---|---|---|---|---|
| 0 | 0.750000 | 0.694445 | 0.693175 | 0.693148 |
| 1 | 0.708334 | 0.693254 | 0.693148 | |
| 2 | 0.697024 | 0.693155 | 0.693146 | |
| 3 | 0.694122 | 0.693147 | ||
| 4 | 0.693391 |
Teniendo en cuenta que el valor exacto de la integral es 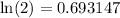 , las aproximaciones conseguidas se pueden considerar como buenas. Las pequeñas diferencias entres sucesiones son debidas al error de redondeo.
, las aproximaciones conseguidas se pueden considerar como buenas. Las pequeñas diferencias entres sucesiones son debidas al error de redondeo.


