La web de Física - Prueba y ejemplos de LaTeX

Cuadro de pruebas

En esta página podrás comprobar las capacidades de LaTeX para componer fórmulas matemáticas. Escribe cualquier comando matemático en el cuadro que encontrarás a continuación y LaTeX creará una imágen del resultado tras compilar en LaTeX. Para incluir fórmulas LaTeX en los foros de La web de Física, deberás introducir el código latex entre las etiquetas [tex] y [/tex] (en este formulario no hace falta).

Puedes copiar a tu discu duro las fórmulas producidas en ésta páginas y utilizarlas libremente para cualquier propósito no comercial. Para hacerlo, haz click con el botón secundario del ratón (el derecho, normalmente) y selecciona la opción Guardar imágen como.... Por favor, no realices enlaces permanentes a la localización de la imágen, ya que se limpia el registro de forma periódica.

Galería de ejemplos

Operaciones aritméticas básicas
a+5b-c(a+b)	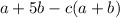$\displaystyle a+5b-c(a+b)$
Fracciones y raíces
\frac{\sqrt a}{a+b} + \sqrt{ \frac{x+5}{x-5} }	$\displaystyle \frac{\sqrt a}{a+b} + \sqrt{ \frac{x+5}{x-5} }$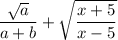
Raíces y más raíces
\sqrt{ 1 + \sqrt{ 1 + \sqrt{ 1 + \sqrt{ 1 + \sqrt{ 1 + \sqrt{ 1 + \sqrt{ 1 + x}}}}}}}	$\displaystyle \sqrt{ 1 + \sqrt{ 1 + \sqrt{ 1 + \sqrt{ 1 + \sqrt{ 1 + \sqrt{ 1 + \sqrt{ 1 + x}}}}}}}$
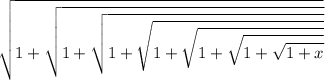Delimitadores
\left( \frac{ 1 }{\sqrt{\frac{x+1}{x-2}}} \right)	$\displaystyle \left( \frac{ 1 }{\sqrt{\frac{x+1}{x-2}}} \right)$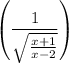
Subíndices (ecuaciones de Einstein)
R_{\mu\nu} - \frac12 g_{\mu\nu} R = \kappa T_{\mu\nu}	$\displaystyle R_{\mu\nu} - \frac12 g_{\mu\nu} R = \kappa T_{\mu\nu}$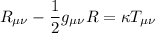
Exponentes
(a+b)^2 = a^2 + 2ab + b^2	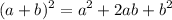$\displaystyle (a+b)^2 = a^2 + 2ab + b^2$
Más exponentes
a^2 - x^{(x^2-2x+1)^{x+1}}	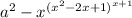$\displaystyle a^2 - x^{(x^2-2x+1)^{x+1}}$
Funciones trigonométricas
\sin(\omega t + \phi_0) \, ,\quad \tan x = \frac{\sin x}{\cos x}	$\displaystyle \sin(\omega t + \phi_0) \, ,\quad \tan x = \frac{\sin x}{\cos x}$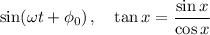
Functiones hiperbólicas
\cosh( \mathrm{argsinh} x ) = \sqrt{1+x^2}	$\displaystyle \cosh( \mathrm{argsinh} x ) = \sqrt{1+x^2}$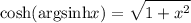
Exponcial
\exp(x) = \mathrm{e}^x = \sum_{n=0}^\infty \frac{x^n}{n!}	$\displaystyle \exp(x) = \mathrm{e}^x = \sum_{n=0}^\infty \frac{x^n}{n!}$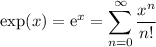
Logaritmos
\ln \left( \frac{f(x)}{\exp\Big( g(x) \Big)} \right) = \ln f(x) - g(x)	$\displaystyle \ln \left( \frac{f(x)}{\exp\Big( g(x) \Big)} \right) = \ln f(x) - g(x)$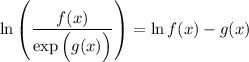
Matrices
\left( \begin{matrix} 0 & -i \\ i & 0 \end{matrix} \right)	$\displaystyle \left( \begin{matrix} 0 & -i \\ i & 0 \end{matrix} \right)$
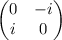Determinantes
\left\| \begin{matrix} a & b \\ c & d \end{matrix} \right\| = ad-bc = 1	$\displaystyle \left\| \begin{matrix} a & b \\ c & d \end{matrix} \right\| = ad-bc = 1$
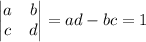Alfabeto griego
\Sigma = \max(\alpha, \beta) - \theta ( \alpha - \beta ) + \Gamma(-\nu)	$\displaystyle \Sigma = \max(\alpha, \beta) - \theta ( \alpha - \beta ) + \Gamma(-\nu)$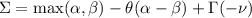
Otros símbolos (I - definición de límite)
\lim_{x\to a} = L \Leftrightarrow \forall \epsilon > 0 ,\ \exists \delta > 0 : \\ \| f(x)- L \| < \epsilon \Rightarrow \| x - a \| < \delta	$\displaystyle \lim_{x\to a} = L \Leftrightarrow \forall \epsilon > 0 ,\ \exists \delta > 0 : \\ \| f(x)- L \| < \epsilon \Rightarrow \| x - a \| < \delta$
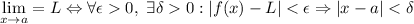Otros símbolos (II - definición de integral)
\int_a^b f(x) \mathrm{d}x = \lim_{n\to \infty} \sum_{k=1}^{n} \frac{b - a}{n} f\left( \left(k - 1/2 \right) \cdot \frac{b - a}{n} \right)	$\displaystyle \int_a^b f(x) \mathrm{d}x = \lim_{n\to \infty} \sum_{k=1}^{n} \frac{b - a}{n} f\left( \left(k - 1/2 \right) \cdot \frac{b - a}{n} \right)$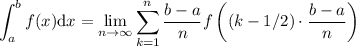
Otros símbolos (III - ecuación de Schödinger)
\hat H \left\| \psi \right> = - \hbar \frac{\mathrm{d}}{\mathrm{d}t} \left\| \psi \right>	$\displaystyle \hat H \left\| \psi \right> = - \hbar \frac{\mathrm{d}}{\mathrm{d}t} \left\| \psi \right>$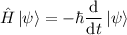
Otros símbolos (IV - conjunto de los números primos)
\mathscr{P} = \left\{ n \in \mathbb{N} \middle\| \forall m \in \mathbb{N} , \, n \div m \not \in \mathbb{N} \right\} \subset \mathbb{N} \subset \mathbb{Z}	$\displaystyle \mathscr{P} = \left\{ n \in \mathbb{N} \middle\| \forall m \in \mathbb{N} , \, n \div m \not \in \mathbb{N} \right\} \subset \mathbb{N} \subset \mathbb{Z}$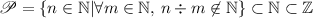
Otros símbolos (V - ley de Gauss)
\oint \vec{E} \cdot \mathrm{d}\vec{S} = \oint \frac{\rho}{\epsilon_0} \mathrm{d}V = \frac{Q}{\epsilon_0}	$\displaystyle \oint \vec{E} \cdot \mathrm{d}\vec{S} = \oint \frac{\rho}{\epsilon_0} \mathrm{d}V = \frac{Q}{\epsilon_0}$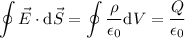
Otros símbolos (VI - ecuaciones de Hamilton)
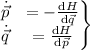\left. \begin{matrix} \dot{\vec p} & = - \frac{\mathrm{d}H}{\mathrm{d}\vec q} \\ \dot{\vec q} & = \frac{\mathrm{d}H}{\mathrm{d}\vec p} \end{matrix} \right\}	$\displaystyle \left. \begin{matrix} \dot{\vec p} & = - \frac{\mathrm{d}H}{\mathrm{d}\vec q} \\ \dot{\vec q} & = \frac{\mathrm{d}H}{\mathrm{d}\vec p} \end{matrix} \right\}$

Acceso rápido