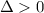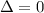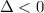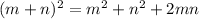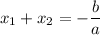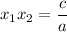La web de Física - Ecuación de segundo grado
Por N30F3B0
Resumen
En el presente documento se dan algunas nociones básicas que se deben de tener en cuenta sobre la ecuación de segundo grado, las propiedades que se muestran están pensadas en que resulten útiles para la resolución de ecuaciones e inecuaciones que contengan formas cuadráticas o reducibles a ellas.Tabla de contenidos
Es una ecuación que tiene la siguente forma:
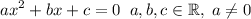
Para encontrar la solución general de esta ecuación hay que tener en cuenta lo siguiente:
Haciendo algunos arreglos a la forma general de la ecuación cuadrática se llega a que:
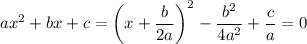
De donde se obtiene finalmente que:
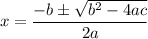
Veamos la siguiente expresión:
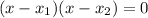
Al desarrollarla se obtiene que:
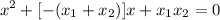
Luego al compararla con la expresión (1) se puede concluir que:
Para poder entenderlo de una mejor manera, llamaremos discriminante a 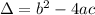 y lo haremos por casos:
y lo haremos por casos:
Se puede ver con facilidad que ambas raíces serán reales y diferentes.
Se obtienen raíces iguales.
No existe solución en los reales.
Sea la expresión:
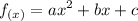
Entonces se puede llegar a verificar que:
- Máximo o mínimo
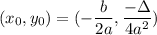 (7)
(7) - Intersección con el eje
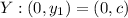
- Intersección con el eje
 : raíces de
: raíces de 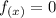
- Además hay que notar que si
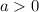 o
o 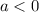 la parábola se abre hacia arriba o hacia abajo respectivamente.
la parábola se abre hacia arriba o hacia abajo respectivamente.
Se llaman puntos críticos de una expresión a aquellos valores en los cuales esta se hace cero o está indeterminada.
Entre dos puntos críticos una expresión solo puede tomar un valor (positiva o negativa).