Simulació Monte-Carlo del Model d'Ising 3-D Antiferromagnètic
Marc Pradas Gené1
Date: 24 de gener de 2005
Partint del model cristal

lí de la teoria de l'estat sòlid, en què els àtoms estan estructurats en xarxes cúbiques
( en el cas més simple ), existeixen dos tipus essencials de metalls: el ferromagnètic i l'antiferromagnètic. Ambdos es caracteritzen per l'aparició d'un ordre en l'organització dels espins dels àtoms en la xarxa per sota d'una certa temperatura;
la diferència entre un i altre està en la forma que tenen d'organitzar-se. El model d'Ising ens dóna una idea intuitiva de com és aquest ordre. Suposem un Hamiltonià del sòlid de la forma:
 |
(1) |
on

són els espins ( amb valor

o

),

el camp aplicat extern,

el nombre total d'àtoms i

la
interacció entre els espins. Si

, estem en el cas ferromagnètic i l'estat d'equilibri ( per

) és aquell en què tots els espins estan en la mateixa direcció, d'altra banda, per

, en l'estat d'equilibri, tots els primers veïs d'un espin amb

són

, i viceversa. Val a dir, però, que per sobre de la temperatura crítica

, els dos estats estan completament desordenats.
Per tal de determinar l'existència d'algun punt crític, s'estudia algunes magnituds físiques susceptibles d'experimentar alguna singularitat o algun canvi significatiu alvoltant d'aquest punt. Abans, però, de mencionar aquestes possibles magnituds d'interés, hem de remarcar quines són les seves variables. Al llarg de tot el treball es farà ús de les anomenades variables reduïdes per l'energia, camp i temperatura:
 |
(2) |
Així doncs, podem començar parlant de la capacitat calorífica. El seu comportament prop del punt crític ve determinat per la llei:
 |
(3) |
on

. Observem una clara singularitat per

, d'on podem afirmar l'existència d'alguna transició de fase. Un resultat important de la física estadísitica és l'anomenat
teorema de fluctuació-dissipació. Aquest ens assegura que la capacitat calorífica, en equilibri, ha de satisfer la relació:
 |
(4) |
on

és l'energia per partícula i el promig s'enten sobre diferents estats d'equilibri. A banda d'aquesta magnitud, el paràmetre per excel·lència que ens indica l'existència d'una transició de fase és l'anomenat paràmetre d'ordre,

, amb la propietat d'anul·lar-se només per

. Pel cas, per exemple, ferromagnètic,

correspon a la magnetització global del sistema, definida com:
 |
(5) |
D'aquesta forma ja podem veure com la magnetització ferromagnètica sempre serà zero en el cas antiferromagnètic, raó per la qual, s'ha de definir un nou paràmetre d'ordre.
El model d'Ising només està resolt analíticament fins a 2-D ( solució d'Onsager ). Per 3-D només podem intentar trobar la solució numèricament o fent aproximacions. Una d'aquestes aproximacions és l'anomenada de camp mig. En aquesta se suposa que els espins es veuen afectats per un camp efectiu promig degut a tota la resta d'espins de la xarxa. D'aquesta forma, l'equació (
1) per un sol espin de la xarxa s'escriu:
 |
(6) |
on

és el nombre de primers veïns i el promig

s'esten per tota la xarxa. Utilitzant nocions de física estadística es pot veure com per

, s'obté una temperatura crítica:
 |
(7) |
Seguint la mateixa filosofia del camp mig, en aquesta aproximació se suposa que l'únic ordre que hi ha és aquell que prové del llarg abast; bàsicament, el que es fa és suposar que la probabilitat de trobar dos espins qualssevol del mateix signe és la mateixa que trobar una parella d'espins igual. Amb aquesta aproximació, es pot trobar una funció de partició per l'Hamiltonià (
1), de tal forma que s'arriba a les equacions :
que ens descriuen l'evolució de la temperatura crítica en funció de la magnetització, evaluada en el punt crític, i el camp. Així doncs, veiem com per camp  recuperem la solució (7).
recuperem la solució (7).
Simulació del model d'Ising
Per descriure correctament un sistema antiferromagnètic hem de definir, doncs, el paràmetre d'ordre del sistema. Per fer-ho dividim la xarxa atòmica en dues subxarxes A i B ( al estar en un sistema cúbic simple tindrem dues bcc), de tal forma que en l'estat fonamental tots els espins de la subxarxa A són positius i els de la subxarxa B són negatius, d'aquesta forma podem definir el paràmetre:
 |
(9) |
on

amb

són els respectius nombre d'espins en la direcció "amunt o avall" de les subxarxes A i B. Amb aquesta definició tenim un paràmetre que s'anul

la per sobre de

, i tendeix a 1 quan

. Quan s'aplica un camp extern, l'orientació provocada és la mateixa per les dues subxarxes, per tant, per sobre de

, quan la interacció antiferromagnètica no és important, també s'anul

la; així doncs és un bon paràmetre d'ordre.
Alhora de calcular el paràmetre d'ordre hem de sumar els espins de les dues subxarxes i restar-ho. Per poder fer-ho considerarem el següent sistema. Suposem una xarxa cúbica de costat

on agafem com a pla

el corresponent a la base del cub, i cada punt del pla el sumem a parelles.
Figure 1:
Subdivisió de la xarxa
|
[Primer pla]![\includegraphics[width=0.49\textwidth,origin=c,angle=0]{xarxa.eps}](img40.png) [Segon pla]
[Segon pla]![\includegraphics[width=0.49\textwidth,origin=c,angle=0]{xarxa2.eps}](img41.png) |
Per conveni escullim el punt

pertanyent a la subxarxa

. D'aquesta forma, per cada pla, i de forma succesiva per tots els punts, sumem les diferents parelles

i

corresponents a la mateixa subxarxa

( veure figura (
1)), i les parelles

i

corresponents a la subxarxa

. Observem, doncs, que si la suma de les coordenades és senar estem a la subxarxa

i si és parell estem a a la subxarxa

.
El mètode utilitzat per fer la simulació és l'algorisme de Metropolis. Una idea senzilla d'aquest mètode és la següent. Partim
d'una configuració inicial aleatòria ( i quan diem aleatòria també ens podem referir a una configuració antiferromagnètica
o ferromagnètica, segons el cas ) i fixem una temperatura; així doncs tenim una energia inicial

. A l'atzar s'escull un lloc de la xarxa i se li canvia l'espin, si aquest canvi provoca un

llavors s'accepta el canvi i la nova energia és

; si

tirem un nombre a l'atzar uniforme

, si

s'accepta el canvi. Si

es rebutja el canvi. Aquest procés es repeteix

cops finalitzant així un pas Monte-Carlo. Per obtindre una estadística suficient es realitzen NMCS passos Monte-Carlo i es fa un promig de les quantitats a mesurar: energia, capacitat calorífica, paràmetre d'ordre, susceptibilitat magnètica,... per tal d'asegurar-nos que els promitjos es realitzen en estats d'equilibri, fem el promig a partir d'un cert nombre de passos Monte-Carlo:

.
Podem veure com varia el paràmetre d'ordre a mesura que creix el nombre de passos Monte-Carlo per diferents temperatures.
Figure 2:
Evolució del paràmetre d'ordre per diferents 
|
![\includegraphics[width=0.60\textwidth,origin=c,angle=0]{xnmcs.eps}](img57.png) |
De la figura (
2) observem com les fluctuacions augmenten a mesura que ens apropem al punt crític. Així doncs, alhora d'escullir el NMCS haurem de tenir en compte en quina temperatura estem; prop del rang de

haurà de ser més gran que lluny del punt crític, per tal asegurar una bona convergència dels valors.
Comencem simulant un sistema cúbic de costat

. El nombre de passos Monte-Carlo utilitzat han estat de 80.000 alvoltant del punt crític i 50.000 en punts més allunyats de

. Les variables estan expresades en les unitats reduïdes (
2). En les següents figures estan representats l'energia, la capacitat calorífica, el paràmetre d'ordre i la magnetització.
Figure 3:
Energia per partícula
Figure 4:
Capacitat calorífica
|
![\includegraphics[width=0.68\textwidth,origin=c,angle=0]{EL202.eps}](img59.png)
![\includegraphics[width=0.68\textwidth,origin=c,angle=0]{CvL202.eps}](img60.png) |
Figure 5:
Paràmetre d'ordre
Figure 6:
Magnetització ferromagnètica
|
![\includegraphics[width=0.61\textwidth,origin=c,angle=0]{PoL202.eps}](img61.png)
![\includegraphics[width=0.61\textwidth,origin=c,angle=0]{mT.eps}](img62.png) |
Podem veure, com era d'esperar, que la magnetització ferromagnètica és pràcticament nul·la en tot el rang. Definint la temperatura crítica aquella en què el paràmetre d'ordre pateix el punt d'inflexió, s'obté una

.
Si fem la mateixa simulació per sistemes més grans ( en les figures (
7) i (
8) es pot observar un sistema de

), observem com la capacitat calorífica augmenta en el punt crític i la corva del paràmetre d'ordre s'aproxima més al valor zero.
Els valors obtinguts per

en tres sistemes diferents han estat:
Table 1:
Temperatures crítiques per diferents tamanys
|
|
Val a dir, que el nombre de passos Monte-Carlo utilitzats per el sistema de

han estat de

, ja que sinó la simulació es feia molt lenta. De tota manera, per obtenir el valor exacte de la temperatura crítica ens farien falta més valors per diferents tamanys, d'aquesta forma es podria fer un ajust (
Finite Size Scaling). Tot i així es pot fer una estimació molt qualitativa, observant a quin punt convergeix el paràmetre d'ordre (figura (
8)), de

.
Figure 7:
Capacitat calorífica per dos tamanys diferents
Figure 8:
Paràmetre d'ordre per dos tamanys diferents
|
![\includegraphics[width=0.68\textwidth,origin=c,angle=0]{CvL20402.eps}](img73.png)
![\includegraphics[width=0.68\textwidth,origin=c,angle=0]{PoL20402.eps}](img74.png) |
Podem fer una comprovació del teorema de fluctuació-disipació (equació (
4)). En la figura (
9) està representat els valors numèrics de la derivada de l'energia per partícula i en linea continua està representat la capacitat calorífica obtinguda a través de la simulació per el sistema de tamany 20.
Quan s'aplica un camp, els espins del sistema tendeixen a alinear-se amb el camp. Es tracta d'un balanç entre la interacció

i la provocada pel camp

. Per temperatures altes (

), la interacció atòmica

és nul·la, per tant, al aplicar un camp els espins s'alinearan en la seva direcció provocant una magnetització ferromagnètica neta diferent de zero, la qual cosa fa que puguem estudiar, també, la susceptibilitat ferromagnètica isoterma definida com:
 |
(10) |
Figure 9:
Comprovació del teorema de fluctuació-dissipació
|
![\includegraphics[width=0.68\textwidth,origin=c,angle=0]{disip.eps}](img77.png) |
Figure 10:
Paràmetre d'ordre per diferents valors de h
|
![\includegraphics[width=0.68\textwidth,origin=c,angle=0]{xh2.eps}](img78.png) |
De la figura (
10) observem com a mesura que augmentem el camp la temperatura crítica disminueix, resultat esperat si ens fixem en l'equació (
8a) de camp mig; d'altra banda, veiem com la susceptibilitat ferromagnètica (figura
11) augmenta fins que s'assoleix la temperatura crítica i torna a disminuir a zero per

altes, quan el desordre es fa més important que l'ordre establert pel camp.
Figure 11:
Susceptibilitat ferromagnètica isoterma per diferents valors de 
|
![\includegraphics[width=0.68\textwidth,origin=c,angle=0]{suscT.eps}](img80.png) |
Estudiem ara el diagrama de fases. Ens situem a

i mirem com varien les diferents magnituds al variar el camp. A la figura (
12) hi està representat els diferents camps per les diferents temperatures crítiques. La linea continua és la solució de camp mig ( equació (
8b)). Ja podem veure una gran discrepància entre una i altra; sobretot en els valors de les temperatures crítiques, encara que ja ens ho podiem esperar; si ens fixem en la solució de camp mig per la temperatura crítica (
7), que en el sitema que estem tractant

, i ho comparem amb la solució obtinguda anteriorment, ja veiem que l'aproximació no és vàlida. No obstant, ens permet de tenir una certa idea qualitativa de com és el comportament. Vege'm sinó, la figura (
13), on hi està representada la temperatura crítica en funció de la magnetització, podem veure un clar comportament paràbolic predit per la teoria de camp mig (equació (
8a)), encara que igual abans, les temperatures no coincideixen. Cal puntualitzar que en totes les mesures obtingudes hi ha el error del sistema finit ( en aquest cas de

), i per tant en els gràfics hi faltaria una barra d'error, tot i així, la discrepància amb la solució camp mig continua sent gran.
I per acabar amb el diagrama de fases i per completitud, en la figura (
14) podem veure com varia la magnetització evaluada en la temperatura crítica al variar el camp.
Figure 12:
Camp en funció de 
|
![\includegraphics[width=0.68\textwidth,origin=c,angle=0]{htc.eps}](img82.png) |
Figure 13:
 en funció de la magnetització
en funció de la magnetització
|
![\includegraphics[width=0.68\textwidth,origin=c,angle=0]{Tcm.eps}](img83.png) |
Figure 14:
Magnetització crítica en funció del camp
|
![\includegraphics[width=0.68\textwidth,origin=c,angle=0]{mh.eps}](img84.png) |
En aquest treball hem pogut calcular la temperatura crítica d'un sistema antiferromagnètic en 3-D, obtenint un valor ( en el cas de

) de

. Hem vist doncs, una discrepància amb la teoria de camp mig, la qual cosa demostra una manca de certesa en l'aproximació. De fet, està demostrat que només per dimensions igual o superiors a 4 és una bona aproximació.
Per tal de saber si la transició és de primer o segon ordre, ens podem fixar, entre altres coses, en el comportament del paràmetre d'ordre. Observant doncs la figura (
5), veiem que

presenta un corva uniforme desde

fins a
0
, la qual cosa ens fa pensar en una transició de fase de segon ordre, ja que en sistemes finits, les transicions de primer ordre presenten una discontinuïtat alvoltant del punt crític.

![\includegraphics[width=0.68\textwidth,origin=c,angle=0]{CvL20402.eps}](img73.png)
![\includegraphics[width=0.68\textwidth,origin=c,angle=0]{PoL20402.eps}](img74.png)



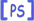





![\includegraphics[width=0.49\textwidth,origin=c,angle=0]{xarxa.eps}](img40.png) [Segon pla]
[Segon pla]![\includegraphics[width=0.49\textwidth,origin=c,angle=0]{xarxa2.eps}](img41.png)
![\includegraphics[width=0.60\textwidth,origin=c,angle=0]{xnmcs.eps}](img57.png)
![\includegraphics[width=0.68\textwidth,origin=c,angle=0]{EL202.eps}](img59.png)
![\includegraphics[width=0.68\textwidth,origin=c,angle=0]{CvL202.eps}](img60.png)
![\includegraphics[width=0.61\textwidth,origin=c,angle=0]{PoL202.eps}](img61.png)
![\includegraphics[width=0.61\textwidth,origin=c,angle=0]{mT.eps}](img62.png)

![\includegraphics[width=0.68\textwidth,origin=c,angle=0]{disip.eps}](img77.png)
![\includegraphics[width=0.68\textwidth,origin=c,angle=0]{xh2.eps}](img78.png)
![\includegraphics[width=0.68\textwidth,origin=c,angle=0]{suscT.eps}](img80.png)
![\includegraphics[width=0.68\textwidth,origin=c,angle=0]{htc.eps}](img82.png)
![\includegraphics[width=0.68\textwidth,origin=c,angle=0]{Tcm.eps}](img83.png)
![\includegraphics[width=0.68\textwidth,origin=c,angle=0]{mh.eps}](img84.png)
