¡Bájatelo! Vídeo DIVX, 10.79 MiB
¡Coméntalo en el foro!

La web de Física - El experimento del huevo

Vídeo de demostración


Descargar vídeo original (10.8MiB)

Resumen

En esta práctica se pretende ejemplificar el principio de la inercia: “todo cuerpo que no esté sometido a fuerza neta mantendrá su estado de movimiento”. Se dispone el montaje tal y como se muestra en la fotografía. El objetivo es introducir el huevo, sano y salvo, dentro del vaso tocando únicamente la cartulina. Se consigue simplemente golpeando la cartulina horizontalmente.

Normalmente, una persona que no conozca los principios de la Física y no haya visto el experimento antes, pensará que golpear la cartulina hará que tanto el canuto como el huevo salgan disparados. No obstante, esto no es así, ya que la fuerza del golpe no se aplica al huevo. Por lo tanto, el principio de la inercia el huevo permanecerá inmóvil, y habiendo perdido su sustento caerá al vaso.

Material necesario

  • Un vaso o un recipiente estanco con la base superior abierta de similares características. Debe llenarse parcialmente de agua para frenar la caída del huevo.
  • Algo de agua para llenar el vaso.
  • Un huevo o un objeto de similares características. Es esencial que quepa con suficiente holgura por la entrada del vaso. Una pelota de golf, por ejemplo, es un buen substitutivo.
  • Cartulina: una pequeña plancha de cartón o cartulina. Su tamaño debe ser suficiente para tapar en su totalidad la obertura del vaso con una holgura suficiente para que pueda ser manipulado sin afectar al resto del material.
  • Canuto: Un pequeño canuto de cartón, un trozo de palo de bandera, o bien una sección de pequeña tubería. Debe poderse mantener en pie sobre uno de sus extremos, y debe poder sostener el huevo sobre su extremo superior.

Montaje experimental

Una vez recopilados los materiales, el montaje experimental es muy sencillo:

  1. Llena el vaso de agua hasta un poco más de la mitad.
  2. Coloca el vaso sobre una superficie horizontal firme, tal como una mesa. Ten en cuenta que la mesa podría mojarse o, si algo sale mal, incluso el huevo romperse en ella, por lo que es aconsejable utilizar algún mantel protector.
  3. Tapa el baso colocando sobre él la cartulina. Procura centrarla lo más posible para maximizar la estabilidad.
  4. Coloca el canuto sobre la cartulina en posición vertical. Debe estar completamente centrado sobre el vaso; conviene comprobarlo mirando desde dos ángulos diferentes.
  5. Con cuidado, coloca el huevo sobre el canuto. Retira los dedos lentamente, asegurándote que permanece en equilibrio.

Procedimiento

Una vez montado el experimento, el procedimiento es muy sencillo: simplemente empujar la cartulina vigorosamente con la mano. Se debe dar un golpe seco completamente horizontal.

Explicación teórica

La situación justo después del golpe se muestra en la siguiente figura;

La fuerza aplicada sobre la cartulina la acelera hacia la izquierda. Dado que el canuto está en contacto directo con la cartulina, existe cierta fuerza de rozamiento sobre el canuto. Dicha fuerza de rozamiento tiene dos efectos:

  • El canuto en su conjunto se acelera hacia la izquierda, según la segunda ley de Newton aplicada al centro de masas.
  • Como la fuerza de rozamiento se aplica en un extremo, el canuto empieza a rotar al rededor de su centro de masas.

Analicemos los dos movimientos del canuto por separado. Primero, la translación de todo el canuto hace que éste se aparte rápidamente de su posición inicial. Segundo, la rotación provocará que el extremo inferior tienda a levantarse (puede que no llegue a conseguirlo, si la fuerza de rozamiento no es lo suficientemente grande, ya que entonces entra en juego la gravedad), mientras que el extremo superior descenderá. Este es uno de los puntos fundamentales: el extremo superior del canuto, donde reposa el huevo, tiende a descender, no a moverse hacia la izquierda. Dado que el canuto no intenta deslizarse sobre la superficie inferior del huevo, no habrá fuerza de rozamiento entre ambos.

Durante el momento del choque, dado que no hay ninguna fuerza sobre el huevo, según el principio de inercia, este permanecerá inmóvil. Entonces entrará en juego la gravedad, que lo hará descender en caída libre hasta el interior del vaso, donde será frenado por el agua.

Algunos cálculos

Resulta sencillo realizar estimaciones acerca de la fuerza mínima que es necesario aplicar. En el tiempo que dure la caída libre del huevo, deben pasar dos cosas:

  • La cartulina debe apartarse completamente del vaso.
  • El canuto debe salir de la perpendicular del vaso.

Sea 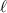\ell la longitud del canuto. El tiempo que durará la caída libre será

\displaystyle t = \sqrt{\frac{2\ell}{g}}\ .
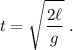
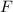Supongamos que la fuerza aplicada con nuestra mano tiene un valor constante, F, y que se aplica a lo largo de una distancia 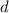d. La conservación de la energía nos da la velocidad que alcanza la cartulina:
\displaystyle v_\text{cart} = \sqrt{\frac{2 F d}{m}}\ .
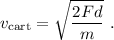
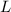Sea L la distancia que tiene que recorrer la cartulina para descubrir completamente el vaso (es decir, la distancia entre el borde derecho de la cartulina y el borde izquierdo del vaso). A partir de ese momento, el movimiento de la cartulina será frenado por el rozamiento con el vaso (dado que el canuto tiende a separarse, no lo tendremos en cuenta en este cálculo). Si el coeficiente de fricción cinético entre el vaso y el cartón es 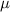\mu. En el tiempo 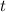t, el desplazamiento de la cartulina debe ser superior a la distancia 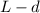L-d, lo que nos da la primera condición:
\displaystyle L-d \le v_\text{cart} t - \frac12 \mu g t^2\ .
Substituyendo todos los datos, tenemos que la fuerza debe cumplir
\displaystyle L-d \le \sqrt{\frac{4F d \ell}{m g}} - \mu \ell\ ,
o lo que es lo mismo
\displaystyle \boxed{ F\ge \frac{m g}{4\ell d} \Big(L-d+\mu\ell \Big)^2 \ . }

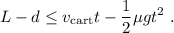
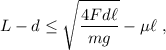
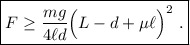
La segunda condición es mucho más fácil de satisfacer. El canuto sólo ha de desplazarse la distancia equivalente al ancho del vaso para apartarse del camino del huevo. Lo que nos interesa, en este caso, es maximizar la fuerza de rozamiento entre el canuto y la cartulina. Por lo tanto, el rozamiento debe ser estático y estar cerca del límite. En la situación límite, la aceleración del centro de masas del canuto —cuyo valor es 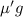\mu' g, donde 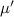\mu' es el coeficiente de rozamiento estático en esta situación— será la misma que la de la cartulina — que a su vez será 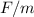F/m. Por lo tanto, la fuerza óptima será

\displaystyle F \lesssim \mu' m g\ .
Para que esta fuerza sea válida, debe cumplir también la anterior condición. Esto nos permite poner una cota inferior al coeficiente de fricción entre el canuto y la cartulina, a saber
\boxed{ \mu' \ge \frac{1}{4\ell d} \Big(L-d+\mu\ell \Big)^2\ .}

Volver a la página principal
© 2003—2025, La web de Física
Dirección de contacto
Créditos