Secciones Destacados

Bájatelo

DOES THE INERTIA OF A BODY DEPEND UPON ITS ENERGY-CONTENT?

BY A. EINSTEIN

September 27, 1905

The results of the previous investigation lead to a very interesting conclusion, which is here to be deduced.

I based that investigation on the Maxwell-Hertz equations for empty space, together with the Maxwellian expression for the electromagnetic energy of space, and in addition the principle that:--

The laws by which the states of physical systems alter are independent of the alternative, to which of two systems of coordinates, in uniform motion of parallel translation relatively to each other, these alterations of state are referred (principle of relativity).

With these principlesas my basis I deduced inter alia the following result (§ 8):--

Let a system of plane waves of light, referred to the system of co-ordinates (), possess the energy ; let the direction of the ray (the wave-normal) make an angle $\phi$ with the axis of of the system. If we introduce a new system of co-ordinates ( $\xi,\eta,\zeta$ ) moving in uniform parallel translation with respect to the system (), and having its origin of co-ordinates in motion along the axis of with the velocity , then this quantity of light--measured in the system ( $\xi,\eta,\zeta$ )--possesses the energy

$\begin{displaymath}l^* = l \frac{1-\frac{v}{c}cos\phi}{\sqrt{1-v^2/c^2}} \end{displaymath}$

where denotes the velocity of light. We shall make use of this result in what follows.

Let there be a stationary body in the system (), and let its energy--referred to the system () be ${\rm E}_0$ . Let the energy of the body relative to the system ( $\xi,\eta,\zeta$ ) moving as above with the velocity , be ${\rm H}_0$ .

Let this body send out, in a direction making an angle $\phi$ with the axis of , plane waves of light, of energy $\frac{1}{2}{\rm L}$ measured relatively to (), and simultaneously an equal quantity of light in the opposite direction. Meanwhile the body remains at rest with respect to the system (). The principle of energy must apply to this process, and in fact (by the principle of relativity) with respect to both systems of co-ordinates. If we call the energy of the body after the emission of light ${\rm E}_1$ or ${\rm H}_1$ respectively, measured relatively to the system () or ( $\xi,\eta,\zeta$ ) respectively, then by employing the relation given above we obtain

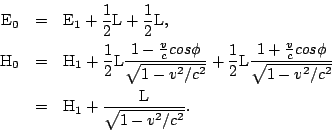
$\begin{eqnarray*} {\rm E}_0 & = & {\rm E}_1 + \frac{1}{2}{\rm L} + \frac{1}{2}{... ...2/c^2}} \\ & = & {\rm H}_1 + \frac{{\rm L}}{\sqrt{1-v^2/c^2}}. \end{eqnarray*}$

By subtraction we obtain from these equations

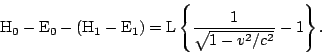
$\begin{displaymath}{\rm H}_0 - {\rm E}_0 - ({\rm H}_1 - {\rm E}_1) = {\rm L}\left\{\frac{1}{\sqrt{1-v^2/c^2}}-1\right\}. \end{displaymath}$

The two differences of the form ${\rm H}-{\rm E}$ occurring in this expression have simple physical significations. H and E are energy values of the same body referred to two systems of co-ordinates which are in motion relatively to each other, the body being at rest in one of the two systems (system ()). Thus it is clear that the difference ${\rm H}-{\rm E}$ can differ from the kinetic energy K of the body, with respect to the other system ( $\xi,\eta,\zeta$ ), only by an additive constant C, which depends on the choice of the arbitrary additive constants of the energies H and E. Thus we may place

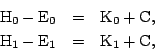
$\begin{eqnarray*} {\rm H}_0 - {\rm E}_0 & = & {\rm K}_0 + {\rm C},\\ {\rm H}_1 - {\rm E}_1 & = & {\rm K}_1 + {\rm C}, \end{eqnarray*}$

since C does not change during the emission of light. So we have

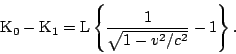
$\begin{displaymath}{\rm K}_0 - {\rm K}_1 = {\rm L}\left\{ \frac{1}{\sqrt{1-v^2/c^2}}-1\right\}. \end{displaymath}$

The kinetic energy of the body with respect to ( $\xi,\eta,\zeta$ ) diminishes as a result of the emission of light, and the amount of diminution is independent of the properties of the body. Moreover, the difference ${\rm K}_0-{\rm K}_1$ , like the kinetic energy of the electron (§ 10), depends on the velocity.

Neglecting magnitudes of fourth and higher orders we may place

$\begin{displaymath}{\rm K}_0 - {\rm K}_1 = \frac{1}{2}\frac{{\rm L}}{c^2}v^2. \end{displaymath}$

From this equation it directly follows that:--

If a body gives off the energy L in the form of radiation, its mass diminishes by ${\rm L}/c^2$ . The fact that the energy withdrawn from the body becomes energy of radiation evidently makes no difference, so that we are led to the more general conclusion that

The mass of a body is a measure of its energy-content; if the energy changes by L, the mass changes in the same sense by ${\rm L}/9\times 10^{20}$ , the energy being measured in ergs, and the mass in grammes.

It is not impossible that with bodies whose energy-content is variable to a high degree (e.g. with radium salts) the theory may be successfully put to the test.

If the theory corresponds to the facts, radiation conveys inertia between the emitting and absorbing bodies.

ABOUT THIS DOCUMENT

This edition of Einstein's Does the Inertia of a Body Depend upon its Energy-Content is based on the English translation of his original 1905 German-language paper (published as Ist die Trägheit eines Körpers von seinem Energiegehalt abhängig?, in Annalen der Physik. 18:639, 1905) which appeared in the book The Principle of Relativity, published in 1923 by Methuen and Company, Ltd. of London. Most of the papers in that collection are English translations by W. Perrett and G.B. Jeffery from the German Das Relativatsprinzip, 4th ed., published by in 1922 by Tuebner. All of these sources are now in the public domain; this document, derived from them, remains in the public domain and may be reproduced in any manner or medium without permission, restriction, attribution, or compensation.

The footnote is as it appeared in the 1923 edition. The 1923 English translation modified the notation used in Einstein's 1905 paper to conform to that in use by the 1920's; for example, denotes the speed of light, as opposed the V used by Einstein in 1905. In this paper Einstein uses L to denote energy; the italicised sentence in the conclusion may be written as the equation `` $m={\rm L}/c^2$ '' which, using the more modern E instead of L to denote energy, may be trivially rewritten as `` ${\rm E}=mc^2$ ''.

This edition was prepared by John Walker. The current version of this document is available in a variety of formats from the editor's Web site:

http://www.fourmilab.ch/

Footnotes

... principles: The principle of the constancy of the velocity of light is of course contained in Maxwell's equations.

Acceso rápido