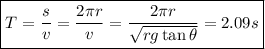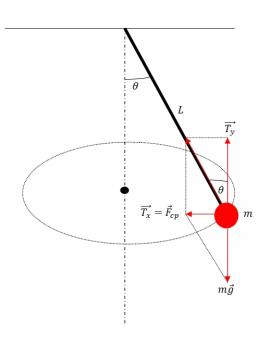
En primer lugar, observemos las fuerzas que actúan sobre el cuerpo que describe la circunferencia:

Figura 1. (Haz click para ver la imagen a tamaño real)

Sea 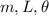la masa del cuerpo, la longitud del hilo y el ángulo que circunscribe con la vertical. Se desea calcular la tensión que soporta la cuerda, así como el valor constante de la velocidad y el período.

Como se dice en el enunciado, el cuerpo describe una circunferencia, en un plano horizontal, por lo que sólo actúa la fuerza centrípeta. Ahora bien, es obvio que ''actúan'' otras fuerzas,como son el peso y la tensión del hilo, con lo cual, la fuerza centrípeta será la resultante de ambas, que de forma vectorial es:

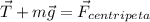
Descomponiendo la tensión en sus componentes horizontal y vertical, la igualdad vectorial anterior se traduce en:

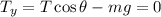
En lo que respecta a la dirección vertical. Observamos que en esta dirección la resultante es cero, lo cual explica la ausencia de movimiento del cuerpo en dicha dirección.

Por otro lado, en la dirección horizontal, tenemos que: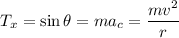

Concluimos que la componente 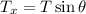es la fuerza centrípeta que hace que el cuerpo describa la circunferencia con una velocidad constante.

Pues bien, de la condición de equilibrio en la dirección vertical, se deduce que la tensión del hilo es igual a:

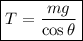
Ahora bien, ¿cuál es el ángulo 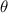? Como se observa en el diagrama, podemos deducir que el ángulo es:

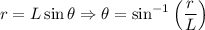
Siendo el radio de la circunferencia que describe. Por tanto, podemos calcular la tensión del hilo:

[ERROR DE LaTeX. Error: 4 ]

Es posible calcular la velocidad, bien sustituyendo el valor obtenido de la tensión en la expresión de la descomposición de la tensión en la dirección vertical, o dividiendo miembro a miembro ambas expresiones:

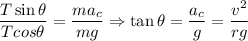
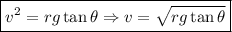
En nuestro caso:

Por último, deseamos calcular el período. Como la velocidad es constante, podemos expresarla como en un movimiento uniforme, es decir:

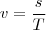
Donde y 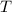es el espacio recorrido, en este caso la longitud de la circunferencia, 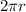y el período de revolución, es decir, el tiempo que tarda en dar una vuelta completa. Por tanto: